Table of Contents
Introduction
Many students get confused in Distinguish between centripetal and centrifugal forces because both appear in circular motion, but they act in opposite directions. This confusion often arises:
- During physics exams
- While driving on curved roads
- When observing clothes spinning in a washing machine
Why understanding the difference is important:
Not just for scoring well in exams, but also to grasp the physics behind everyday activities.
Let’s break it down simply and clearly:
[articlepage]
Circular Motion – Basics Before Comparing Forces
Definition:
Circular motion refers to the motion of an object along a circular path. Understanding this is crucial, especially when comparing centripetal and centrifugal forces.
Key Points to Know:
1️⃣ Circular Path:
The object moves around a central point. The radius (r) is the distance from the center to the object.
2️⃣ Velocity & Acceleration:
Even if the speed of the object is constant, its direction keeps changing. This results in an inward acceleration called Centripetal Acceleration.
3️⃣ Types of Circular Motion:
- Uniform Circular Motion (UCM): Speed remains constant; only direction changes.
- Non-Uniform Circular Motion (NUCM): Both speed and direction change.
4️⃣ Importance:
Understanding these basics is essential to know how forces act in circular motion:
- Centripetal Force (CF): Keeps the object on its circular path.
- Centrifugal Force (CeF): Apparent force felt in a rotating (non-inertial) frame.

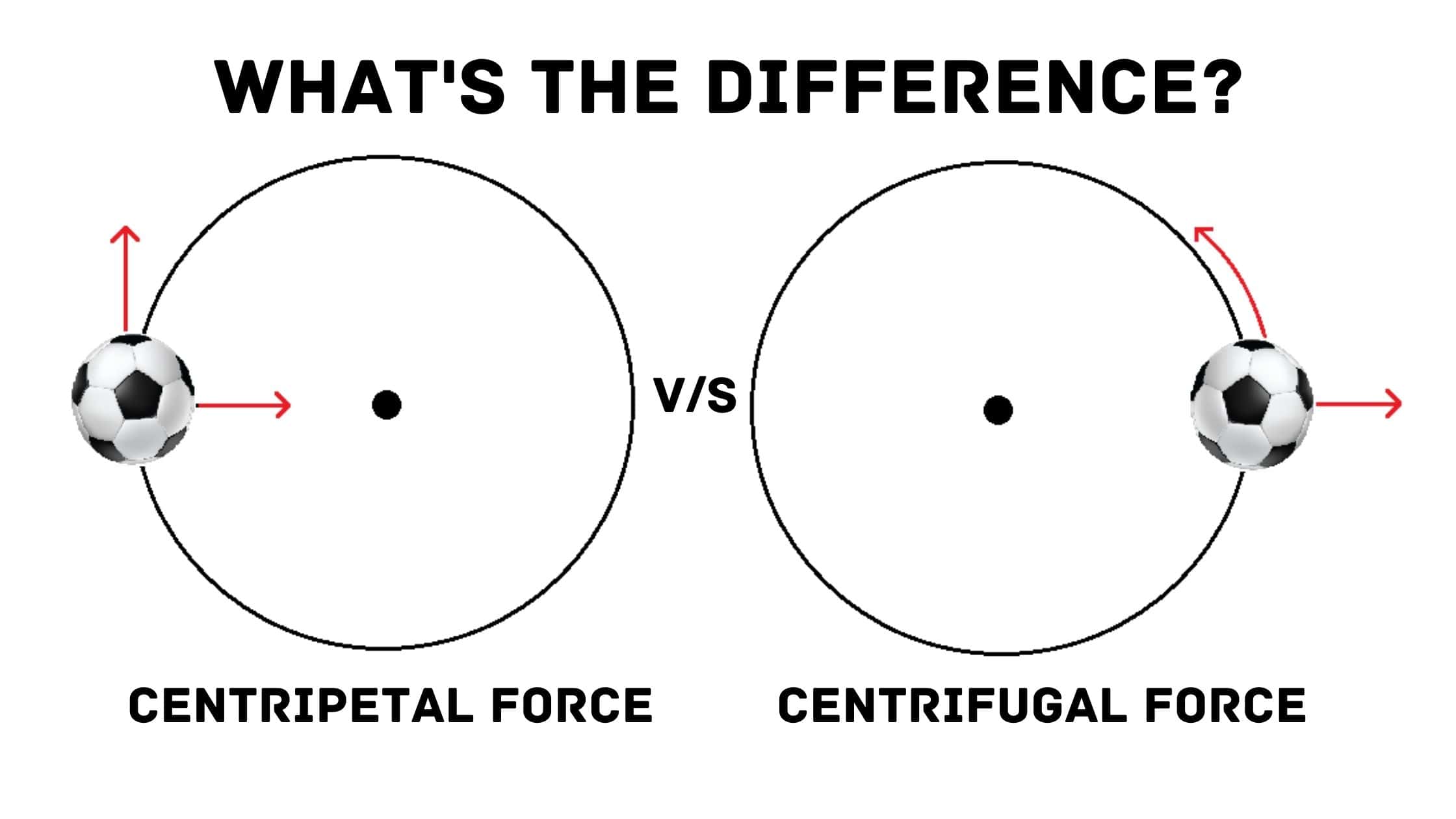
What is Centripetal Force?
Centripetal Force: Simple Explanation
Definition:
Centripetal force is the real force that pulls an object toward the center of a circle when it moves along a circular path. It keeps the object on the curved path and prevents it from flying off in a straight line.
🎯 Everyday Example:
Imagine swinging a ball tied to a rope.
- Your hand pulls the rope inward, preventing the ball from flying outward.
- This inward-pulling force is the centripetal force.
- If the rope breaks, the ball would move in a straight line, not along the curve.
💡 Note:
When you feel an outward “push” while a car turns, that is not a real force. It is the centrifugal force, experienced due to inertia.
⚡ Main Formula:
F = (m × v²) / r
Where:
- F = centripetal force (in Newtons, N)
- m = mass of the object (kg)
- v = speed (m/s)
- r = radius of the circular path (m)
➡ More speed (v) or mass (m) → greater force needed
➡ Larger radius (r) → less force needed
📏 Unit:
Centripetal force is measured in Newtons (N).
➡ Direction:
Always toward the center of the circle, perpendicular to the velocity. It continuously changes the object’s direction.
✅ Example Problem:
A car of 1000 kg mass moves on a circular track of 50 m radius at a speed of 20 m/s.
F = (m × v²) / r = (1000 × 20²) / 50 = (1000 × 400) / 50 = 8000 N
🔹 The car requires 8000 N inward force (provided by road friction) to stay on the curve.
💡 Quick Recap:
- Centripetal force keeps objects on a circular path.
- Depends on mass, speed, and radius.
- Always acts toward the center of the circle.
What is Centrifugal Force?
[articlepage]
Definition: Centrifugal Force
Centrifugal force is not a real force. It only feels as if a force is pushing an object away from the center, but in reality, no such force exists.
🎯 Everyday Example:
Imagine sitting on a merry-go-round. When it spins fast, you feel as if you are being pushed outward.
This sensation is called centrifugal force.
In fact, this force is only experienced in a rotating frame, which is why it is called a pseudo force.
⚡ Unit:
The unit of centrifugal force is also Newton (N).
🧮 Formula:
Even though it is not a real force, its magnitude can be calculated as:
F = (m × v²) ÷ r
Where:
- F = centrifugal force (N)
- m = mass (kg)
- v = velocity (m/s)
- r = radius of the circle (m)
👉 This force always appears outward and acts in the opposite direction to the centripetal force.
🎯 Direction:
The centrifugal force always points outward.
It is not a real force but is felt due to inertia.
🔍 Frames of Reference:
- Inertial Frame (stationary observer): Only the centripetal force acts as a real force.
- Non-Inertial Frame (rotating observer): The person feels as if a force is pushing outward—this is the centrifugal force.
🌏 Real-Life Examples:
1️⃣ Weight difference on Earth:
The Earth spins constantly. At the equator, the higher rotational speed makes objects feel slightly lighter. This effect is absent at the poles.
2️⃣ Bicycle turn:
When taking a sharp turn, the cyclist leans inward.
👉 This counters the outward pull sensation experienced as centrifugal force.
3️⃣ Car turn:
Passengers feel as if they are being pushed outward when the car takes a turn.
👉 This is the experience of centrifugal force.
4️⃣ Railways near the equator:
Due to faster rotation near the equator, trains experience a slight outward effect. Engineers consider this while designing tracks.
💡 Key Points to Remember:
- Centrifugal force is a perceived force, not real.
- It always points outward from the center.
- It exists only in a rotating (non-inertial) frame.
Frame of Reference in Physics: Inertial vs Non-Inertial
A frame of reference is the viewpoint from which we observe and measure motion. Understanding the difference between inertial and non-inertial frames is crucial, especially for forces like centrifugal force.
Why Centrifugal Force Appears Only in Rotating Frames
1️⃣ Inertial Frame:
- An inertial frame is non-accelerating, like standing on the ground.
- In this frame, only real forces act on an object.
- In circular motion, centripetal force is the only real force pulling the object toward the center.
- No centrifugal force exists here.
2️⃣ Non-Inertial Frame:
- A non-inertial frame is accelerating or rotating, like a turning car or a spinning merry-go-round.
- The observer feels as if a force is pushing the object outward.
- This apparent force is called centrifugal force.
- It is not a real force, but a pseudo force introduced to explain motion from a rotating frame.
Observers Inside and Outside a Rotating System
Outside Observer (Inertial Frame):
- Sees the object pulled toward the center only by centripetal force.
- Object moves along a circular path, and no outward force acts.
Inside Observer (Non-Inertial Frame):
- Feels an outward force acting on the object.
- Example: A passenger in a car taking a left turn feels pushed to the right.
- In reality, this is only the effect of inertia, perceived as centrifugal force.
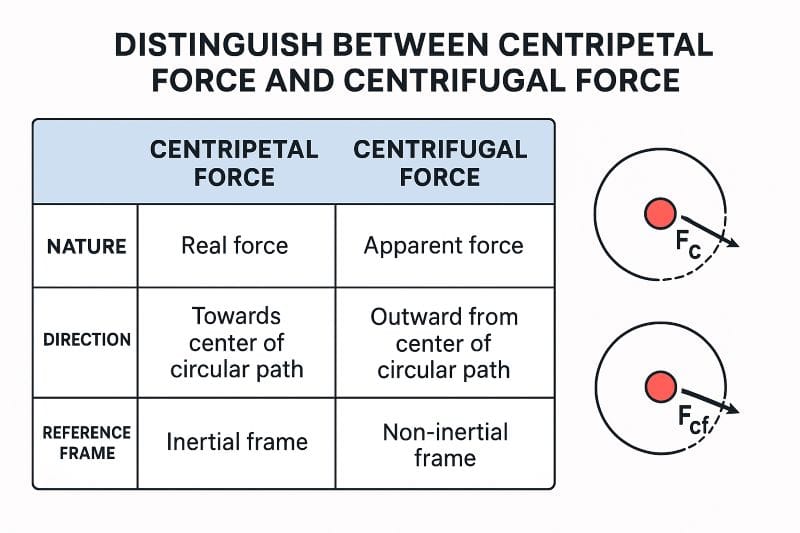
distinguish between centripetal force and centrifugal force
When an object moves along a circular path, two types of forces are often discussed:
- Centripetal Force → Pulls the object toward the center (real force)
- Centrifugal Force → Appears to push the object away from the center (apparent/pseudo force)
[articlepage]
Here’s a simple, exam-friendly comparison of Centripetal vs Centrifugal Force 👇
| Feature | Centripetal Force | Centrifugal Force |
|---|---|---|
| Meaning | Real force that keeps an object moving in a circular path toward the center. | Pseudo force that appears to push an object outward when viewed from a rotating frame. |
| Nature | Real force (e.g., tension in a string, gravity, friction). | Imaginary/pseudo force—felt but not actually applied. |
| Direction | Always toward the center of the circular path. | Always away from the center. |
| Reference Frame | Observed from an inertial frame (stationary or ground-based observer). | Felt only in a non-inertial (rotating) frame. |
| Cause | Arises from physical interactions like tension, gravity, or friction. | Perceived due to inertia—the body resists change in motion. |
| Formula | F = m × v² / r | F = − m × v² / r (negative sign indicates outward direction) |
| Examples | Ball swung on a string, gravity keeping planets in orbit, friction on a turning car. | Feeling pushed outward in a turning car, slightly reduced weight at the equator, water moving to edges in a spinning bucket. |
Effect of Speed, Radius, and Mass on Centripetal and Centrifugal Force
In circular motion, forces are crucial to keep an object moving along its curved path. The two main forces are:
- Centripetal Force – Real force pulling toward the center
- Centrifugal Force – Apparent force felt outward in a rotating frame
Here’s how speed (v), radius (r), and mass (m) affect these forces:
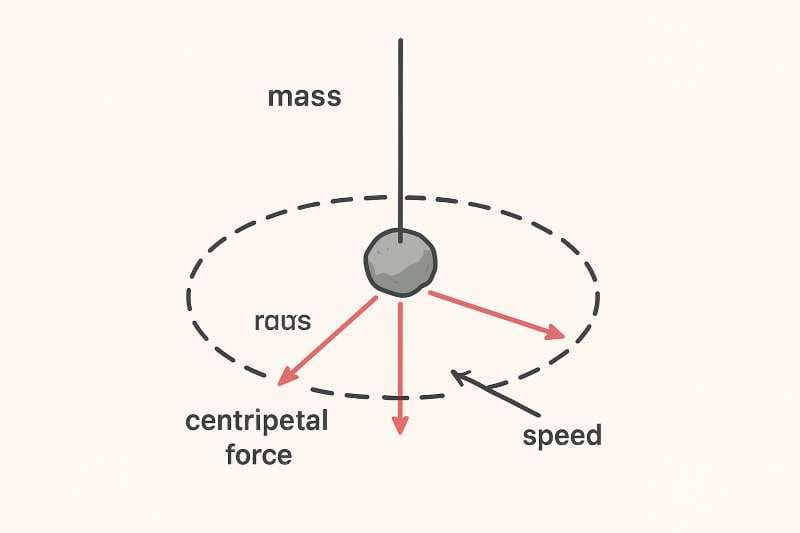
1️⃣ Effect of Speed (v)
- Centripetal Force ∝ v²
- If the speed doubles, the required centripetal force quadruples.
- This explains why fast-moving vehicles need more friction or properly banked roads to negotiate turns safely.
2️⃣ Effect of Radius (r)
- Centripetal Force ∝ 1 / r (inversely proportional to radius)
- Smaller radius requires a stronger inward pull.
- Example: Sharp curves on roads are more dangerous than wide curves at the same speed.
3️⃣ Effect of Mass (m)
- Centripetal Force ∝ m
- The heavier the object, the more centripetal force is required.
- Example: A heavy truck experiences much larger force on a turn compared to a small car at the same speed and radius.
🔑 Key Formula
F = m × v² / r
Where:
- m = Mass of the object
- v = Speed of the object
- r = Radius of the circular path
💡 Insights from the formula:
- Higher mass or higher speed → more force required
- Larger radius → less force required
Solved Examples: Centripetal and Centrifugal Force
Example 1 – Stone on a Rope
Question:
A stone of mass 0.5 kg is tied to a rope and revolves in a horizontal circle of radius 1.2 m at a speed of 4 m/s. Find the centripetal force.
Solution:
Centripetal Force,
F = m × v² / r
F = 0.5 × 4² / 1.2 = 8 / 1.2 ≈ 6.67 N
Answer: 6.67 N toward the center
Example 2 – Car on Circular Track
Question:
A car of mass 1200 kg moves on a circular track of radius 50 m at a speed of 20 m/s. Find the centripetal force.
Solution:
F = m × v² / r
F = 1200 × 20² / 50 = 1200 × 400 / 50 = 480000 / 50 = 9600 N
Answer: 9600 N toward the center
Example 3 – Rotating Space Station for Artificial Gravity
Question:
A rotating space station generates artificial gravity equal to Earth’s gravity (9.8 m/s²) at its edge. The radius of the edge is 100 m. What should be the speed at the edge?
Solution:
Centripetal acceleration, a_c = v² / r
Set a_c = g = 9.8 m/s²
v² = a_c × r = 9.8 × 100 = 980
v = √980 ≈ 31.3 m/s
Answer: The edge should move at ≈ 31.3 m/s to simulate Earth’s gravity.
Real-Life Applications: Engineering and Astronomy
[articlepage]
Banked Roads, Roller Coasters, and Vehicle Safety
Centripetal force plays a key role in designing safe transportation systems.
- Banked Roads:
The tilt of the road ensures that vehicles do not rely solely on friction when turning. Cars can take turns at higher speeds safely, reducing the risk of skidding. - Roller Coasters:
Centripetal force keeps passengers securely in their seats during fast loops and sharp turns. Engineers carefully design speed, radius, and height to provide both thrilling and safe experiences. - Everyday Driving:
Understanding centripetal force enhances vehicle safety, particularly when navigating curves at varying speeds.
Satellite Orbits and Planetary Motion
In astronomy, centripetal force explains the motion of satellites and planets.
- Artificial Satellites:
Satellites orbit the Earth because gravity provides the necessary centripetal force. - Balance of Speed and Radius:
If a satellite moves too fast, it escapes orbit; too slow, it falls back to Earth. - Planetary Motion in the Solar System:
Planets maintain stable orbits around the Sun due to a balance between gravitational pull (inward) and the planet’s tendency to move outward.
This balance keeps planets in stable orbits for billions of years.
Everyday and Engineering Applications
| Application | Centripetal Force (Real) | Centrifugal Effect (Felt) |
|---|---|---|
| 🎢 Roller Coaster | Keeps cars on track during loops and turns | Riders feel pushed outward |
| 🧪 Centrifuge Machines | Pulls blood or liquids inward to separate components | Heavy particles move outward, light ones separate |
| 🚗 Banked Roads | Provides inward pull for safe turns at high speed | Drivers feel pushed outward during turns |
| 🛰️ Satellites & Space Stations | Gravity keeps satellites in orbit | Rotating space stations create artificial gravity at the rim |
[articlepage]
Common Misconceptions About Centripetal and Centrifugal Forces
Why You Feel Pushed Outward in a Turning Car
When a car takes a sharp turn, passengers often feel as if they are being pushed outward. This is not caused by any real outward force. Instead, your body naturally wants to continue moving in a straight line (inertia). The car turns inward, but your body resists the change in direction. The car seat or door provides the centripetal force that changes your motion, creating the sensation of being pushed outward.
Centrifugal Force vs. Inertia – The Truth
A common misconception is that centrifugal force is a real physical force. In reality, it is a pseudo force felt only in a rotating (non-inertial) frame of reference. What people experience as centrifugal force is actually inertia—objects resist changes to their state of motion.
From the perspective of a stationary Earth (inertial frame), only the centripetal force acts on the object, keeping it in circular motion.
Centrifugal force is merely perceived because your body tries to continue straight while the path curves.
Similarities Between Centripetal and Centrifugal Forces
Centripetal and centrifugal forces may seem opposite, but in circular motion, they are two aspects of the same phenomenon. Simply put, their similarities are:
| Similarity | Description |
|---|---|
| Always appear in circular motion | Both are observed when an object moves along a curved path, such as a swing, roller coaster, or satellite orbiting Earth. |
| Depend on mass, speed, and radius | Both forces increase if the object is heavier (m), faster (v), or moving in a smaller circle (r). |
| Interconnected | Centripetal force pulls inward; the centrifugal effect is felt outward. The outward “feeling” occurs only because the inward pull keeps the object in circular motion. |
| Expressed by the same formula | Magnitude is the same: F = m × v² / r (centripetal inward, centrifugal outward in a rotating frame). |
| Not directly measurable | We observe their effects (e.g., tension in a rope or outward push on a ride) rather than measuring them directly. |
Historical Development of Centripetal and Centrifugal Forces
The concepts of centripetal and centrifugal forces have deep roots in the history of physics. In the 17th century, scientists began formally studying circular motion and the forces involved.
- Johannes Kepler (1609–1619): While studying planetary motion, Kepler described that planets move in elliptical paths around the Sun. He proposed that some force from the Sun pulls planets inward, though he did not define it precisely.
- René Descartes (1640s): Descartes coined the term centrifugal force to explain the tendency of objects in circular motion to move outward. He connected this idea to mechanical philosophy.
- Christiaan Huygens (1659): Huygens provided a mathematical definition of centripetal force. He showed that the inward force required to maintain circular motion depends on the object’s speed and the circle’s radius.
- Isaac Newton (1687): In his famous Principia Mathematica, Newton formalized centripetal force as a real inward force. He described centrifugal force as only an empirical effect, felt in a rotating frame due to inertia.
Legacy
These historical contributions laid the foundation of modern mechanics. Today, the concepts of centripetal and centrifugal forces are vital in engineering, space science, and physics education.
Conclusion
Centripetal and centrifugal forces are two aspects of circular motion. Centripetal force is a real force that pulls an object inward, keeping it on a circular path, whereas centrifugal force is a felt or apparent force that seems to push outward, appearing only in a rotating (non-inertial) frame.
Both forces have the same magnitude: F = m × v² / r, and depend on the object’s mass, speed, and radius.
Key Takeaways:
- Centripetal Force: Always inward, real.
- Centrifugal Force: Outward effect, only experienced.
- Understanding the difference is crucial for applications in daily life, engineering, and celestial motion.
FAQ
What is Centripetal Force?
Centripetal force is the force that pulls an object toward the center when it is moving in a circle. Without this force, the object would fly off in a straight line. It keeps the object moving along a curved path.Give examples of Centripetal Force.
Here are some simple examples:
The moon goes around the earth because of centripetal force.
When you spin a top, it stays in its circular path because of centripetal force.
If you tie a stone to a string and swing it around, the force pulling the stone toward your hand is the centripetal force.Does Centripetal Force increase with speed?
Yes, it does!
When something moves faster in a circle, the pull toward the center becomes stronger. So, more speed means more centripetal force is needed to keep it moving in a circle.Does Centripetal Force increase with radius?
No, it actually gets weaker.
If the circle is bigger (more radius), the force needed to keep the object on the curved path becomes smaller. So, the larger the circle, the less centripetal force is required.Can centripetal and centrifugal forces exist at the same time?
Yes, they can. When something moves in a circle, two forces seem to show up. One pulls it inward—that’s the centripetal force. The other feels like it’s pushing outward—that’s the centrifugal force. They happen at the same time, but they come from different ideas. One is real, and one just feels real.Are these forces only used in circular motion?
Mostly, yes. Centripetal and centrifugal forces happen when things move in circles. But they can also appear in spinning and rotating objects, like a spinning wheel or a merry-go-round. Anywhere something is turning, these forces can show up. Why do passengers feel pushed outward in a turning car?
Passengers feel an apparent outward push due to centrifugal force in the rotating frame of the car. In reality, the seat provides the inward centripetal force to keep them moving in a curved path.
Which force is used in washing machines?
The centrifugal force (apparent outward force) is used to separate water from clothes in washing machine dryers.
Which force acts on a satellite?
A satellite in orbit is kept in its path by the centripetal force of gravity pulling it toward the Earth.
Which one is a real force?
Centripetal force is the real physical force, whereas centrifugal force is only an apparent force experienced by observers in a rotating frame.
What is the main difference between centripetal and centrifugal force?
Centripetal force is a real inward force that keeps an object in circular motion, while centrifugal force is a pseudo outward force felt in a rotating (non-inertial) frame.