Table of Contents
Understanding Angular and Linear Velocity
Imagine you are spinning a wheel. The speed at which the wheel turns is called angular velocity. It tells us how fast something is turning around a fixed point. For example, if a fan is spinning, its blades are moving in a circle. Angular velocity helps us know how quickly they are turning.
Now think about a car moving straight on a road. The speed at which the car moves from one place to another is called linear velocity. It tells us how fast something is moving in a straight line.
So, angular velocity is about spinning or turning, while linear velocity is about moving straight.
But here’s something interesting — when something turns in a circle, like the wheel of a bicycle, it actually has both types of speed!
There is a simple link between them:
- Linear velocity = Angular velocity × Radius
This means, the faster something spins (angular velocity), and the bigger the circle it spins in (radius), the faster it moves forward (linear velocity).
Derivation of Relation Between Linear Velocity and Angular Velocity
Let us imagine a small object moving in a circular path. The object is going around in a circle, just like how a fan blade moves or how the hands of a clock rotate.
Let the radius of the circle be r.
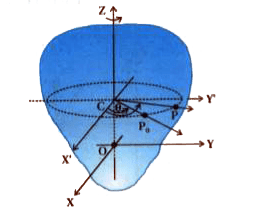
Now, when the object moves from one point to another along the circular path, it covers some distance. This curved distance is called S, and it is the linear displacement of the object.
The angle made by this movement at the center of the circle is called θ (theta). This is the angular displacement.
Let’s think about a moving object. When it moves, it covers some distance. The change in the distance it moves is called ΔS, and the time it takes to move that distance is Δt.
The speed at which the object moves in a straight line is called linear velocity. We write it as v and find it by dividing the distance moved by the time taken:
v = ΔS / Δt
Now, if the object is moving in a circle, it turns through an angle. The change in this angle is called Δθ, and it also happens over a time Δt.
The speed of this turning motion is called angular velocity, written as ω, and it is:
ω = Δθ / Δt
Imagine the object is moving around a circle with a radius r. The distance it travels along the edge of the circle (the arc length) is related to the angle it turns through by:
S = r × θ (Equation 1)
We also know from earlier that linear velocity is:
v = ΔS / Δt
If we replace S from Equation 1, the formula becomes:
v = Δ(r × θ) / Δt
Since r is constant (the radius does not change), we can write:
v = r × (Δθ / Δt)
But from the definition of angular velocity:
ω = Δθ / Δt
So, putting it all together:
v = r × ω
This is the key relation showing how linear velocity (v) and angular velocity (ω) are connected through the radius (r) of the circle.
This is the beautiful and simple relation between linear velocity and angular velocity. It tells us:
Linear velocity = Radius × Angular velocity
Relation Between Linear Velocity and Angular Velocity
Let’s imagine a body that is turning around a fixed line—like how the blades of a fan spin around the center. This motion is called rotational motion. In this motion, every part of the body moves in a circle, and the center of that circle lies on the axis (the fixed line it is rotating around).
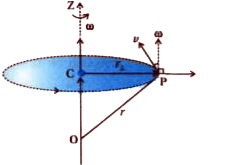
Angular Velocity
Now, take one point on that body—let’s call it Point P. As the body rotates, Point P goes around in a circle. The distance between Point P and the axis of rotation is called the radius.
When this point moves, it covers some angle in a given time. This angle is called angular displacement. If the point rotates by an angle Δθ in time Δt, the average angular velocity is:
Angular velocity = Δθ / Δt
As we look at a smaller and smaller moment of time, we get the instantaneous angular velocity, which is written as:
ω = dθ / dt
This tells us how fast the point is turning at any given moment. Angular velocity is written with the Greek letter omega (ω) and it shows how fast something is rotating.
Linear Velocity and Angular Velocity
Even though the point is rotating, it is also moving in a straight path along the circle at every instant. This movement along the path is called linear velocity, written as v.
There is a simple and clear relation between linear velocity and angular velocity:
v = ω × r
Here:
- v is linear velocity (how fast the point moves along the circle),
- ω is angular velocity (how fast it rotates),
- r is the radius (distance from the axis).
So, if the point is far from the center (a bigger radius), it will move faster along the edge. And if it is right on the axis (radius is zero), the point will not move at all. That means the linear velocity is zero at the center.
This relation is true for every part of a rigid body (a solid body that doesn’t bend) when it rotates. Every point spins with the same angular velocity, but the linear velocity changes depending on how far the point is from the axis.
Final Thoughts
This simple formula v = ω × r helps us understand how rotation works. It connects spinning (angular motion) with straight-line movement (linear motion).
It shows that when something spins, how fast each part moves depends on both how fast it spins and how far it is from the center.
Difference Relation Between Linear Velocity and Angular Velocity
Let’s understand two very important types of motion: angular velocity and linear velocity.
🌪️ Angular Velocity
- Angular velocity tells us how fast something is turning or rotating.
- It is the speed of rotation around a center or an axis.
- Imagine the hands of a clock. As they move around the center, that’s angular velocity.
- It does not change with the position on the circle – it stays the same as long as the rotation speed is constant.
- It is measured in degrees per second or radians per second.
- We show it using the Greek letter ω (omega).
- Angular velocity is not only about circular motion. In fact, circular motion is just one way we can observe angular velocity.
🏃 Linear Velocity
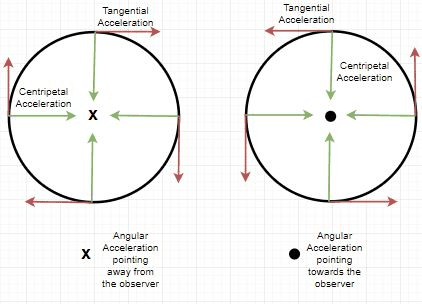
- Linear velocity tells us how fast something is moving in a straight line.
- It is the speed of movement from one point to another.
- Imagine a car driving on a straight road – that’s linear velocity.
- In circular motion, linear velocity means how fast a point on the edge of a spinning object is moving along the circle’s path.
- It can change at different points if the object speeds up or slows down.
- It is measured in meters per second (m/s).
- We show it with the letter v.
🧠 Easy Example
Think of a spinning wheel:
- The center of the wheel is rotating – this is angular velocity.
- The outer edge of the wheel is moving around – this is linear velocity.
Both are part of the same motion, but they describe it in different ways!
What is Angular Velocity?
Angular Velocity tells us how fast something is spinning or turning around a center point.
If you spin a wheel, Angular Velocity tells you how quickly the wheel is turning.
- It does not care about how far something moves.
- It only cares about how fast it turns or rotates.
👉 Simple words:
Angular Velocity is the speed of rotation.
What is Linear Velocity?
Linear Velocity tells us how fast something is moving in a straight line.
If a car is driving on a road, Linear Velocity tells us how quickly it is going from one place to another.
In a circular motion (like a spinning wheel), the Linear Velocity shows how fast a point on the edge of the wheel is moving around the circle.
👉 Simple words:
Linear Velocity is the speed of moving forward.
Main Difference
| Feature | Angular Velocity | Linear Velocity |
|---|---|---|
| What it shows | Speed of turning | Speed of moving |
| Direction | Around a center | Along a path or circle’s edge |
| Changes | Usually stays the same in circular motion | Changes depending on the position |
| Unit | Degrees per second or radians per second | Meters per second (m/s) |
| Symbol | Greek letter ω (omega) | Small v |
| Formula | ω = Δθ / Δt or ω = 2π / t | v = Δs / Δt or v = 2πr / t |
Advantages of Having Definitions and Relations Between Linear Velocity and Angular Velocity
Understanding science becomes a lot easier when students clearly know what the words mean. In every subject, especially science, there are some important terms that we must understand well. If we know their definitions, then learning becomes simple and fun. The same is true for the terms linear velocity and angular velocity.
These two terms may look very different at first. But when we understand what they mean and how they are connected, everything starts making sense. That’s why having both the definition and the relation between linear and angular velocity is so helpful.
When students learn the meaning of these words in simple language, they don’t feel scared or confused. Instead, they feel confident. If the explanation is clear, they can easily remember the definitions. Not only that, they can also understand the difference between the two, and how they are connected.
For example, once a student understands what linear velocity means (movement in a straight line) and what angular velocity means (movement in a circle), then they can also understand how one affects the other.
Having clear definitions:
- Helps students build a strong science base
- Makes learning faster and easier
- Helps in solving problems with better understanding
- Clears confusion between similar terms
- Builds confidence in students
So, when we give students easy-to-understand definitions and also show how the terms are related, they learn better, faster, and with more joy. It’s like giving them a key to open many doors in science.
Why is Angular Displacement an Axial Vector?
Imagine a particle moving around in a circle. It goes round and round — that’s called circular motion. As it moves, it covers an angle. This angle is called angular displacement.
Now, the question is:
Why is this angular displacement called an axial vector?
Let’s understand this step by step:
When something moves in a circle, there are two things we can notice:
- It moves along the edge of the circle — this is called linear displacement (s).
- It also makes an angle as it moves — this is called angular displacement (θ).
So, angular displacement tells us how much the particle has turned from its starting position.
But here’s the special thing:
Even though the particle is moving in a flat circle, the direction of this turning (angular displacement) is not on the circle — it’s along the axis, which is like an invisible stick coming out from the center of the circle.
This direction (along the axis) is what makes it an axial vector. It doesn’t point where the particle is going, but it points around which axis it is turning — either up or down, like a screw being twisted.
The Relation Between Linear and Angular Displacement
Let’s say:
- The radius of the circle is r.
- The angle made (in radians) is θ.
Then, the distance moved along the edge (the arc) is:
s = r × θ
…..(1)
This is how angular displacement and linear displacement are connected.
What is Linear Velocity?
Linear velocity means how fast the particle is moving along the edge of the circle.
It is written as:
v = s / t
…..(2)
Where:
- v is the linear velocity,
- s is the linear displacement,
- t is the time taken.
What is Angular Velocity?
Angular velocity means how fast the angle (θ) is changing — or how fast the particle is turning.
It is written as:
ω = θ / t
…..(3)
Where:
- ω (omega) is the angular velocity,
- θ is the angular displacement,
- t is the time taken.
So, to sum up:
- Angular displacement is an axial vector because its direction is along the axis of rotation.
- It tells us how much angle is covered by a particle in circular motion.
- And it connects directly to how fast something is moving in a circle.
Relation Between Linear Velocity and Angular Velocity
Imagine a wheel turning around its center. There is a point P on the wheel that is also moving as the wheel spins. This point goes in a circular path.
We know the distance S moved by the point on the wheel is:
S = r × θ
Where:
- r is the radius (distance from the center to the point),
- θ is the angle turned by the wheel (in radians).
If we divide both sides by time t, we get:
S / t = (r × θ) / t
This becomes:
v = r × (θ / t)
Now, θ / t is the angular velocity, which we call ω (omega).
So, we get:
v = r × ω
This is the relation between linear velocity (v) and angular velocity (ω).
What This Means:
- v is the linear velocity – how fast the point is moving along the circle.
- ω is the angular velocity – how fast the wheel is spinning.
- r is the radius – the distance from the center to the moving point.
Important Points:
- The point at the center of the wheel does not move, so its linear velocity is zero.
- As the point moves away from the center, its linear speed gets faster.
- The farthest point, at the edge of the wheel (on the circumference), has the highest linear velocity.
- The direction of linear velocity is always along a straight line touching the circle (called a tangent).
In Simple Words:
If a wheel spins faster (more ω), the point on it also moves faster (more v).
If the point is farther from the center (more r), it also moves faster.
So we say:
Linear velocity (v) = Radius (r) × Angular velocity (ω)
Angular Velocity and Linear Velocity – Easy Explanation
When something moves in a circle, like a fan blade or a wheel, it has two types of speed:
- Angular Velocity (ω) – How fast it turns, or rotates.
- Linear Velocity (v) – How fast it moves along the edge of the circle.
Now, there is a simple and beautiful relation between them:
v = r × ω
Here’s what this means:
- v is the linear velocity (how fast the object is moving around the circle).
- r is the radius (how far the object is from the center of the circle).
- ω is the angular velocity (how fast the object is spinning).
So, the farther you are from the center, the faster you move in a straight line, even if the turning speed (angular velocity) stays the same.
🚴 Real-Life Feeling:
Imagine you’re sitting on a merry-go-round.
- If you’re sitting close to the center, you don’t move very fast.
- If you’re sitting at the edge, you fly around quickly!
Even though everyone is turning at the same angular speed, your linear speed is faster if you’re farther from the center.
🔄 Key Points:
- Linear velocity is not the same everywhere on the circle.
- At the center, it is zero.
- Between the center and edge, it is medium.
- At the edge, it is maximum.
- But angular velocity stays the same for all points on a rigid circular object. Everything rotates together.
✅ Conclusion:
Whenever something moves in a circle:
- Its linear velocity depends on how far it is from the center.
- Its angular velocity tells us how fast it turns.
And the beautiful link between them is:
Linear Velocity = Radius × Angular Velocity
v = rω
Easy Example:
Imagine a bicycle wheel that has a radius of 0.5 meters.
Suppose the wheel is spinning at 4 radians per second (this is angular velocity).
We want to find out how fast a point on the edge of the wheel is moving (this is linear velocity).
👉 Using the formula:
v=ω×r=4×0.5=2 m/s
The wheel is moving at 2 meters per second.
Example:
Let’s say:
- A wheel has a radius of 2 meters
- It is spinning with an angular velocity of 4 radians per second
Now, using the formula:
v = ω × r
v = 4 × 2
v = 8 meters per second
So, the point on the edge of the wheel is moving at 8 meters per second.
FAQ
I am an Electrical Engineer with qualifications in ITI, Diploma, and B.Tech. I have worked as an ITI college instructor for 3 years and have over 5 years of hands-on experience in the electrical field. The information shared on this website is based on trusted electrical engineering textbooks such as P.S. Bimbhra, B.L. Theraja, V.K. Mehta, and real-world practical experience.