Table of Contents
Circular motion is everywhere around us—the rotation of a ceiling fan, the spinning of a wheel, the moon orbiting the Earth, or the Earth revolving around the Sun.
Understanding it is not only essential for students and engineers but also fascinating for anyone who wants to know how and why an object moves along a circular path.
In this guide, you will find:
- Definition – What circular motion is and its types.
- Key Formulas – Essential equations for motion, acceleration, and force.
- Derivation – Step-by-step origin of the formulas.
- Real-Life Examples – Like a rotating fan, a roller coaster turn, or a satellite orbit.
- Solved Questions – To understand concepts and practice applications.
- Practice Problems – To test yourself and prepare for exams.
What Is Circular Motion?
Circular motion means the movement of an object along a circular path.
When an object repeatedly moves along the same circular path, it is called circular motion.
Think of a clock’s hands, a ceiling fan, or a bicycle wheel—all of these rotate in a circular path. This is a circular motion.
When an object moves along a circle, it always stays at a fixed distance from the center.
This distance is called the Radius (R)
Concepts of Circular Motion
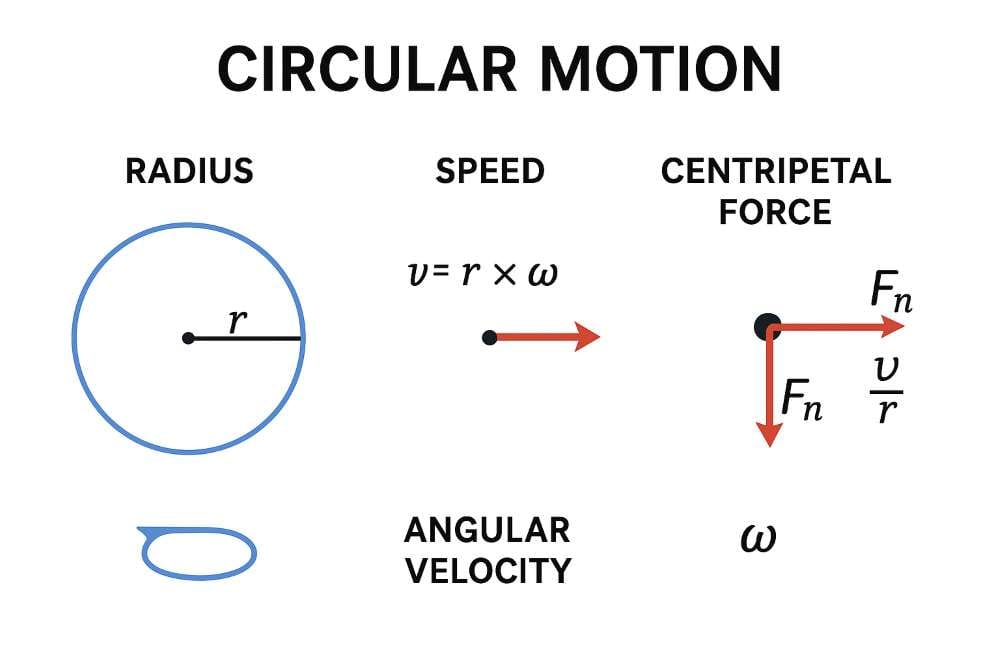
1. Radius (त्रिज्या, r)
The distance from the center to the object. It determines the size of the circle.
Radial (Radius) Vector
A radial vector is a straight line from the origin (center) to the current position of a moving point.
- It shows the direction and distance of that point from the center.
- As the point moves, the direction of this vector changes continuously.
👉 In short:
The radial vector tells where the particle is and how far it is from the origin at any instant.
2. Uniform Circular Motion
When an object moves around a circle at a constant speed, it performs uniform circular motion.
- The object travels around a fixed center.
- The speed stays constant, but the direction of velocity changes every moment.
- A centripetal force is required to keep it in the circular path.
Key Features
- Radius Vector: A line from the center to the object remains the same length but rotates as the object moves.
- Velocity (v): Always along a tangent to the circle.
- Acceleration: Even with constant speed, the changing direction means the object has centripetal acceleration toward the center.
💡 Example:
A ball tied to a string was whirled at a steady speed.
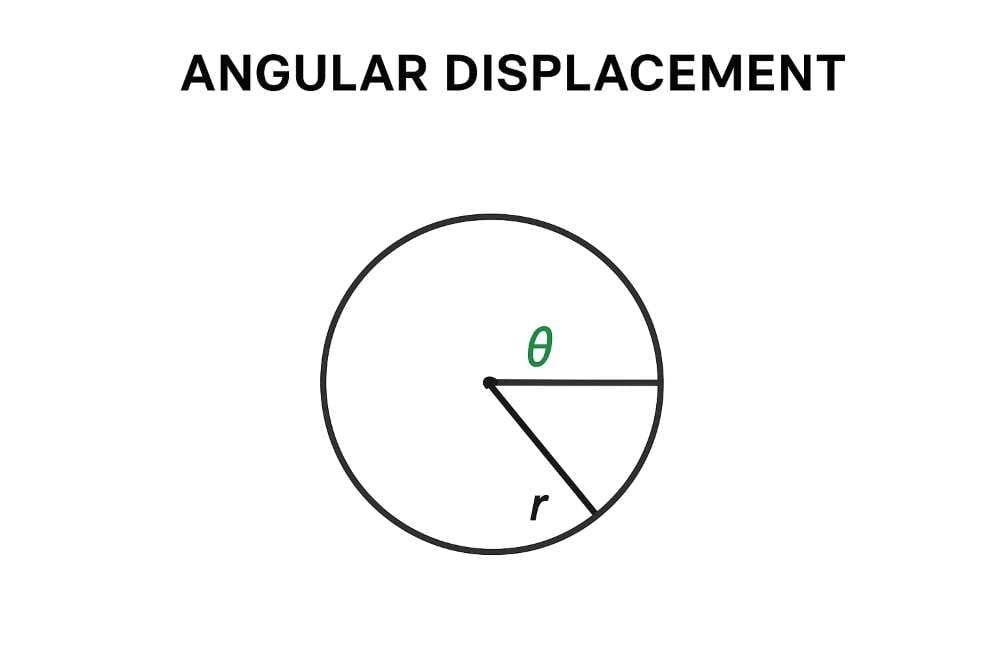
3. Angular Displacement
Angular displacement measures the angle a radius vector sweeps out as the object moves along the circle.
Formula
If the object moves from angle θ₁ at time t₁ to angle θ₂ at time t₂:
Δθ = θ₂ – θ₁
Relation to Linear Displacement
If the object travels a small arc length Δs on a circle of radius r, then
Δθ = Δs / r
(or simply Angle = Arc / Radius)
Unit
- Radian (rad): The angle made when the arc length equals the radius.
- 1 rad ≈ 57.3°
4. Speed (वेग, v)
How fast the object is moving. It can be constant (uniform circular motion) or variable (non-uniform circular motion)
Speed & Velocity (वेग और गति)
In circular motion, the velocity of an object is always tangential to the circle.
It is perpendicular to the radius connecting the object to the center.
If the angle θ changes with time:
vₓ = −R sinθ × (dθ/dt)
vᵧ = R cosθ × (dθ/dt)
Speed (गति):
v = R × (dθ/dt)
Angular Speed (कोणीय वेग):
ω = dθ/dt
Therefore,
v = R × ω
5. Period (आवर्तकाल, T)
Time taken to complete one full revolution.
T = 1 / f
6. Frequency (आवृत्ति, f)
Number of revolutions completed per second.
f = 1 / T
💡 Memory Tip:
If an object spins faster, the period (T) decreases and the frequency (f) increases.
Types of Circular Motion
1️⃣ Uniform Circular Motion (समान परिपथ गति)
When an object moves around a circle with constant speed throughout the revolution.
The magnitude of speed remains constant, but the direction continuously changes.
Example: A Satellite orbiting Earth, rotating like a merry-go-round.
👉 Example: A toy train moving on a circular track without speeding up or slowing down.
2️⃣ Non-Uniform Circular Motion (असमान परिपथ गति)
When an object’s speed varies at different points of the circular path.
The speed of the object varies (faster or slower) while moving along the circular path.
Example: A Car on a curved road with changing speed.
👉 Example: A bicycle turning on a curved road.
| Type | Description | Example |
|---|---|---|
| Uniform Circular Motion (UCM) | Speed remains constant but direction changes. | Satellite orbiting Earth, merry-go-round |
| Non-Uniform Circular Motion | Speed changes (accelerates or decelerates) while moving in a circle. | Speed remains constant, but direction changes. |
🔑 Key Point: Even in UCM, velocity is not constant because its direction changes continuously.

Angular and Linear Quantities
Angular Velocity (कोणीय वेग)
Definition:
In circular motion, the rate of change of angular displacement with time is called angular velocity.
Simple Explanation:
Angular velocity tells us how fast an object is rotating around a point.
Symbol:
Greek letter ω (omega)
Formulas:
- Average Angular Velocity:
ω = Δθ / Δt - Instantaneous Angular Velocity:
ω = dθ / dt
- Unit: radian per second (rad/s)
- Dimension: [T⁻¹]
Vector Nature (Direction):
- Determined by the Right-Hand Thumb Rule:
- Anticlockwise → Thumb points up/out of plane
- Clockwise → Thumb points down/into plane
Special Cases:
- One Complete Revolution:
ω = 2π / T (where T = time for one revolution) - n revolutions per second:
ω = 2π n
Summary:
- What it is: Speed of rotation about a point
- Symbol: ω
- Formula: ω = dθ / dt
- Unit: rad/s
- Direction: Perpendicular to the plane of rotation (right-hand rule)
Linear Velocity (रैखिक वेग)
Definition:
In rectilinear motion, the rate of change of position of an object with respect to time is called linear velocity.
Simple Explanation:
Linear velocity tells us how fast and in which direction an object is moving along a straight path.
Formulas:
- Average Linear Velocity:
v = Δs / Δt
(where Δs = displacement, Δt = time interval) - Instantaneous Linear Velocity:
v = ds / dt
(velocity at a particular instant)
Unit and Dimension:
- Unit: meter per second (m/s)
- Dimension: [L T⁻¹]
Vector Nature:
Linear velocity is a vector quantity, meaning it has both:
- Magnitude: How fast the object is moving
- Direction: The direction in which the object is moving
Example:
If a toy car moves 2 meters in 1 second, its average linear velocity = 2 m/s
Summary:
- What it is: Rate of motion along a straight path
- Symbol: v
- Formulas: v = Δs / Δt, v = ds / dt
- Unit: m/s
- Vector: Has both magnitude and direction
Linear and angular measurements are related:
| Quantity | Angular Form | Linear Relation |
|---|---|---|
| Displacement | θ (radians) | s = rθ |
| Velocity | ω (rad/s) | v = rω |
| Acceleration | α (rad/s²) | aₜ = rα (tangential) |
Acceleration (त्वरण)
Tangential Acceleration (स्पर्शरेखीय त्वरण)
Meaning:
It indicates that the speed of the object is changing — either increasing or decreasing.
Visualization: Imagine the object is being pushed forward or pulled backward along the path.
Formula:
aₜ = R × α
where α (alpha) = angular acceleration = rate of change of angular velocity.
- Present only in non-uniform motion when speed changes.
a_t = dv/dt
Total acceleration:
a = √(a_c² + a_t²)
Centripetal Acceleration (केन्द्राभिमुख त्वरण)
Meaning:
This is always present, even if the object is moving at constant speed.
It pulls the object toward the center to prevent it from flying off the circular path.
Formula:
aₙ = v² / R = R × ω²
where v = linear velocity, ω = angular velocity, R = radius.
Direction: Always toward the center, along the radius of the circle.
Important Formulas
| Quantity | Formula |
|---|---|
| Angular velocity | ω = θ / t |
| Linear speed | v = r ω |
| Centripetal acceleration | a_c = v² / r |
| Centripetal force | F_c = m v² / r |
| Period & Frequency | T = 2π r / v, f = 1 / T |
Forces in Circular Motion (परिपथीय गति में बल)
To keep an object moving in a circular path, a centripetal force is required.
Formula:
Fₙ = m v² / r = m r ω²
Where:
- m = Mass of the object
- v = Linear velocity
- r = Radius of the circle
- ω = Angular velocity
Possible Sources of Centripetal Force:
- Tension: e.g., a stone tied to a rope
- Friction: e.g., a car on a curved road
- Gravity: e.g., planets orbiting the sun
- Normal Reaction: e.g., roller coaster loop
Direction: This force always acts toward the center of the circle to maintain circular motion.
Energy in Circular Motion (परिपथीय गति में ऊर्जा)
1. Kinetic Energy (गतिज ऊर्जा, KE)
The kinetic energy of an object moving in a circle is:
KE = ½ m v²
Where:
- m = Mass of the object
- v = Linear speed
Key Points:
- If the motion is uniform (Uniform Circular Motion), KE remains constant because the linear speed does not change.
2. Work Done (कार्य)
- Work is done only when tangential acceleration changes the speed of the object.
- If the object moves with pure uniform circular motion, no net work is done.
- This means the centripetal force only changes direction, not speed, so there is no change in kinetic energy.
Time Period and Speed in Circular Motion
Time Period (T)
The time taken for one complete revolution of a circle.
Total distance of one round: 2πr
Speed along the circle: v
To find the time period, we use:
Time Period (T) = Total distance of one round / Speed
The distance of one full round of a circle is:
2πr
So,
T = 2πr / v
If we use v = ω × r, we can also write:
T = 2π / ω
So,
T = 2πr / v
Using the relation v = ω r, we can also write:
T = 2π / ω
Motion of a Rigid Body
When a rigid body spins about an axis:
- Every point moves in a circle, covering the same angle in the same time.
- All points have the same angular velocity (ω).
- Their linear velocity (v) depends on the distance from the axis.
Key Relation
A point at radius r has linear speed:
v = r × ω
Where:
- v = linear velocity (m/s) – tangent to the circle
- r = radius (m) – distance from center
- ω = angular velocity (rad/s) – same for all particles
Directions (Right-Hand Rule)
Imagine a flat spinning disc:
- r → points from the center to the particle
- ω → points upward, perpendicular to the disc (for anticlockwise spin)
- v → tangent to the circle, in the direction of motion
Banked Curves in Circular Motion
1. Introduction
A banked curve is a road or track tilted at an angle (θ) to allow vehicles to take turns safely at higher speeds.
In circular motion, a vehicle requires centripetal force to stay on its curved path. On a banked road, this force comes from a combination of normal force and friction.
Real-life examples: Highways, race tracks, roller coasters, airport runways.
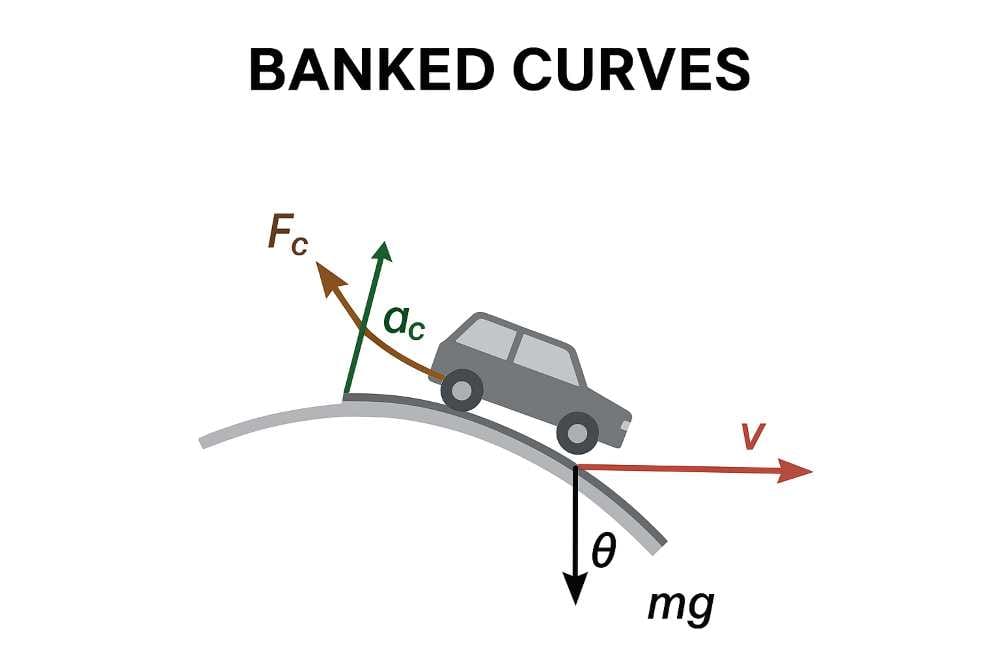
2. Forces on a Vehicle in a Banked Curve
When a vehicle moves on a banked turn, four main forces act on it:
- Centripetal Force (Fₖ): Keeps the vehicle moving in a circle.
- Normal Force (N): Perpendicular to the banked surface.
- Friction (f): Along the plane; helps when speed ≠ ideal.
- Weight (mg): Acts vertically downward.
3. Ideal Speed on a Frictionless Banked Curve
If friction is negligible, the ideal speed is:
v₍ideal₎ = √(r g tanθ)
Where:
- r = radius of the curve
- g = acceleration due to gravity
- θ = banking angle
Example: For a curve of radius r = 50 m banked at θ = 30°,
v₍ideal₎ = √(50 × 9.8 × tan30°) ≈ 16 m/s (≈ 58 km/h)
4. Banked Curves with Friction
When the speed ≠ is ideal, friction helps maintain the circular path.
- Maximum safe speed:
v₍max₎ = √[r g (tanθ + μ) / (1 − μ tanθ)]
- Minimum safe speed:
v₍min₎ = √[r g (tanθ − μ) / (1 + μ tanθ)]
Where μ = coefficient of friction.
These formulas ensure vehicles safely negotiate turns even at varying speeds.
5. Applications of Banked Curves
- Highways & Flyovers: Reduce risk of skidding and accidents.
- Race Tracks: Enable high-speed turns without losing grip.
- Roller Coasters & Amusement Rides: Provide thrill and safety during sharp curves.
Common Scenarios & Applications of Circular Motion
1. Conical Pendulum (कोनिकल पेंडुलम)
A bob moves in a horizontal circle while the string traces out a cone shape.
It shows the balance between tension (T) and gravity (mg).
2. Vertical Circular Motion (ऊर्ध्वाधर परिपथीय गति)
Example: Roller coaster loops, a pendulum passing through the top point.
At the highest point, a minimum speed is required so that the object does not fall.
3. Banked Curves (ढलान वाले वक्र)
Used for safe turning at high speeds.
It reduces dependence on friction, allowing vehicles to take turns smoothly.
4. Real-World Applications (वास्तविक जीवन में अनुप्रयोग)
- Astronomy: Planetary orbits, motion of satellites.
- Engineering: Rotating machinery, turbines, centrifuges.
- Daily Life: Ceiling fans, washing machine spin cycles, amusement park rides.
Practice Problems on Circular Motion (With Solutions)
Problem 1: Tension in a Rotating String
Question:
A 0.5 kg stone tied to a string rotates in a horizontal circle of radius 1 m at 4 m/s. Find the tension in the string.
Solution:
The tension provides the centripetal force:
Fₐ = m v² / r = (0.5 × 4²) / 1 = 8 N
✅ Answer: Fₐ = 8 N
Problem 2: Minimum Friction for a Car on a Curve
Question:
A car of mass 1000 kg moves around a curve of radius 50 m at 20 m/s. Find the minimum coefficient of friction required to prevent skidding.
Solution:
Centripetal force: Fₐ = m v² / r
Normal force: N = m g
Friction provides the centripetal force: Fₐ = μ N
μ = v² / (r g) = 20² / (50 × 9.8) ≈ 0.82
✅ Answer: μ ≈ 0.82
Problem 3: Speed of a Satellite
Question:
A satellite completes one circular orbit of Earth in 90 minutes. If the orbital radius is r = 6.8 × 10⁶ m, find its speed.
Solution:
Time period: T = 90 minutes = 5400 seconds
Orbital speed:
v = 2 π r / T = (2 π × 6.8 × 10⁶) / 5400 ≈ 7.9 km/s
✅ Answer: v ≈ 7.9 km/s
7. Final Summary – All Key Formulas in One Place
| Type | Linear (Straight Path) | Angular (Circle) |
|---|---|---|
| Position | s | θ |
| Velocity | v = ds/dt | ω = dθ/dt |
| Acceleration | a = dv/dt | α = dω/dt |
| Connection | s = Rθ | v = Rω |
| a = Rα | ac = v²/R = Rω² |
In Simple Words:
- Circular motion means moving around a circle.
- We can measure the position using distance or angle.
- The object always wants to go straight, but a force (like the string in our toy example) pulls it toward the center to keep it on the path.
- There is always a pull toward the center called centripetal acceleration.
- If the object changes speed, there’s also tangential acceleration along the circle’s edge.
FAQ
What are the characteristics of Uniform Circular Motion?
Uniform circular motion has some very special features:
The object moves in a circle.
Its speed stays the same all the time.
Even though the speed doesn’t change, the direction does change again and again.
Because the direction changes, the velocity also changes.
The velocity is always pointed along the path, like a line touching the circle.
The acceleration always points towards the center of the circle.
This also means the force is always pulling the object towards the center.What is circular motion?
A: Circular motion means moving in a circle. If something goes round and round on the same path, like a fan or the hands of a clock, it is in circular motion.Does the object go at the same speed in circular motion?
A: Sometimes yes, sometimes no. If the object moves in a circle at the same speed, it is called uniform circular motion. If the speed changes, it is called non-uniform circular motion.Is there any force acting in circular motion?
A: Yes. There is a special force called centripetal force. It always pulls the object towards the center of the circle. Without this force, the object would fly away in a straight line.What is the direction of motion in circular motion?
A: The direction keeps changing as the object moves around the circle. That’s why even if speed is the same, the motion is still changing.