What is Wheatstone Bridge?2 Derivation, formula, exam useful important facts

What is Wheatstone Bridge?

A Wheatstone Bridge is a simple electrical circuit used to find an unknown resistance. It works like a balance scale. When the bridge is balanced, we can easily calculate the missing value.

The circuit has four resistors:

• Two are known
• One is unknown (the one we want to find)
• One can be adjusted (a variable resistor)

These resistors are connected in a diamond shape, like a bridge. That’s why it’s called a “bridge” circuit.

When everything is set just right and the bridge is balanced, no current flows through the center part of the circuit. This tells us that the values on both sides are equal, and then we can use a simple formula to find the unknown resistor.

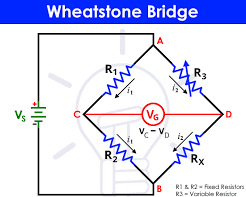
Construction of a Wheatstone Bridge

A Wheatstone Bridge is a type of electrical circuit used to measure an unknown resistance. It is made up of four parts called “arms.”

• Two of these arms have resistors with known values.
• The other two arms have one unknown resistor and one adjustable resistor (we can change its value).

Along with these, the circuit also includes:

• A galvanometer (a device that shows if current is flowing),
• And a battery or power source that gives energy to the circuit.

The battery is connected between two points, called point A and point B.
The galvanometer is connected between two other points, called point C and point D.

When the circuit is working, electric current flows through it. The amount of current that flows through the galvanometer depends on the difference in electric pressure (called potential difference) between point C and point D.

What is the Wheatstone Bridge Principle?

The Wheatstone Bridge is a smart and simple way to measure unknown resistance in a circuit. It works on a very clear idea: when the bridge is balanced, no current flows through the center part of the circuit.

Imagine a square made of four resistors. Two of them are known, one is adjustable, and one is the unknown resistance you want to find. In the middle, there’s a device called a galvanometer, which shows if any current is flowing.

Here’s how it works:
When the ratio of the two known resistors is equal to the ratio of the adjustable and unknown resistors, the galvanometer shows zero current. This means the bridge is balanced.

At that moment, you can use a simple formula to find the unknown resistance. It’s like a perfect balance on a scale—when everything is just right, there’s no movement.

If the bridge is not balanced, the galvanometer will show some current. You can then adjust the variable resistor until the current becomes zero. Once that happens, you know the bridge is balanced and you’re ready to calculate the unknown value.

In short, the Wheatstone Bridge helps us find an unknown resistance by comparing it with known values, using the principle of balance and no current flow in the middle wire.

Wheatstone Bridge Derivation

The Wheatstone Bridge is a smart and simple electric circuit. It was created by an English engineer named Wheatstone. He made it to help measure the exact value of an unknown resistance – something that resists the flow of electricity.

Let’s understand how it works.

The Wheatstone Bridge has four resistors. Think of resistors like little roadblocks for electric current. These resistors are connected in the shape of a diamond or a square. Here’s what each side of that diamond has:

• P and Q are two resistors whose values we already know.
• R is another resistor that we can adjust (a variable resistor).
• X is the unknown resistor – this is what we are trying to find.

These four resistors are connected together in a loop, with points named A, B, C, and D. Imagine drawing a square and labeling the corners like that.

Now, here’s how we test it:

• A battery is connected across corners A and C.
• A special device called a galvanometer is connected across corners B and D, with a small key (like a switch) to control the flow.
• The galvanometer checks whether any current is passing between B and D.

Here’s the magic part:
We adjust the resistor R until the galvanometer shows zero current. This means the bridge is balanced.

When that happens, we can use a simple rule to find the value of the unknown resistor X using the known values of P, Q, and R.

This setup is called a bridge because the galvanometer connects (or bridges) two opposite points of the diamond.

Imagine you have four resistors arranged in a diamond shape. Two of these resistors, called P and Q, have fixed values. Another resistor, R, can be changed. The fourth resistor, X, is the unknown one we want to find.

Now, there’s a special device called a galvanometer connected across the diamond to detect any current flowing through it. We adjust the resistor R until the galvanometer shows zero current. When this happens, we say the bridge is balanced.

At the balanced point, something interesting happens: the voltage (or electric pressure) at two points in the circuit—let’s call them B and D—is exactly the same. Because of this, no current flows through the galvanometer.

Since there’s no current through the galvanometer, the current flowing through resistors P and Q is the same as the current flowing through R and X, respectively.

This gives us two important equalities based on voltage drops (how much the voltage decreases across each resistor):

• The voltage drop across P equals the voltage drop across R.
• The voltage drop across Q equals the voltage drop across X.

From these equalities, we get:

I1×P=I2×R

and

I1×Q=I2×X

Here, I1 and I2 are the currents flowing through the resistors.

By dividing these two equations, we find:

P/Q=R/X

Rearranging this, the value of the unknown resistor X is:

X=Q×R/P

Since the values of P, Q, and R are known, we can easily calculate X.

Important note: This calculation only works when the bridge is balanced—that means no current is flowing through the galvanometer, and points B and D have the same voltage.

example

Let’s check if the Wheatstone bridge shown in the picture is balanced. After that, we will find the voltage VT​ across the 0.2 A current source in two different cases:

1. When the 200-ohm resistor is replaced by a wire (which means a short circuit).
2. When the 200-ohm resistor is removed completely (which means an open circuit).

Important points to know:

• The bridge has four key points, named A, B, C, and D. Each point is where two resistors meet.
• A device called a galvanometer connects two opposite points, usually B and D. The battery connects the other two points, A and C.
• The resistors labeled P and Q are called the ratio arms. These are usually chosen to keep a specific ratio, like 1:1, 10:1, or 100:1.
• The resistor called RRR is the rheostat arm. This resistor can be changed smoothly over a wide range, for example, from 1 ohm to 1,000 ohms or even up to 10,000 ohms.

Solution

The Wheatstone bridge is balanced when the product of the resistances in one pair of opposite arms is the same as the product in the other pair. In other words, if you multiply the resistance of R1 by R4, and multiply R2 by R3, these two results should be equal for the bridge to be balanced. So, R1 × R4 = R2 × R3 means the bridge is balanced.

1. When 200 Ω resistor is shorted.

Now, let’s look at what happens when the 200-ohm resistor, called R5, is removed or replaced by a wire (which is called a short circuit). When this happens, the circuit changes. Instead of the original Wheatstone bridge, the circuit now looks like a combination of resistors in series and parallel.

In this new circuit, R1 and R2 are connected in parallel, and R3 and R4 are also connected in parallel. Then, these two groups are connected in series with each other. This new setup can be simplified step-by-step.

When you do the math, the total resistance of the whole circuit adds up to 135 ohms. This is found by adding the resistance of the two parts in series: 90 ohms plus 45 ohms.

Finally, if the current source provides 0.2 amperes (A), the voltage across the circuit is calculated by multiplying the current by the total resistance. So, voltage V = 0.2 × 135 = 27 volts (V).

, RT = 90 + 45 = 135 Ω.
The voltage across 0.2 A current source is
VT = I RT = 0.2 × 135 = 27 V

2. when 200 Ω resistor is open-circuited.

Imagine we have a bridge circuit, and we take out the 200-ohm resistor by replacing it with an open connection (meaning no current can flow through that part). When we do this, the circuit changes into something called a series-parallel circuit.

Here’s what that means: The resistors R1 and R3 are connected one after another (in series), and this combination is connected side-by-side (in parallel) with another pair, which is R2 and R4, also connected in series.

If you look at the simplified version of this circuit, the total resistance of the whole setup can be found by calculating the combined effect of these resistors. When we do the math, the total resistance, called RT, comes out to be 135 ohms.

Now, if there is a current source pushing 0.2 amps through this circuit, we can find the voltage across the current source by multiplying the current by the total resistance. That gives us 0.2 amps × 135 ohms = 27 volts.

One interesting thing to notice here is that whether we replace the 200-ohm resistor with a short circuit (a wire) or an open circuit (no connection), the voltage across the current source stays the same.

RT = 180×540/180+540 = 135 Ω

In this case:

Voltage across 0.2 A current source, VT = I RT = 0.2 A × 135 Ω = 27 volts (V)

Wheatstone Bridge formula

Let’s take a look at the Wheatstone Bridge circuit and understand how it works.

In the circuit:

• R1 and R2 are the known resistances. We already know their values.
• R3 is an adjustable resistance. That means we can change it as needed.
• Rx is the unknown resistance—the one we are trying to find.
• G is a galvanometer. It’s a device that shows if current is flowing through it.
• A battery is connected between points P and R to supply power.

There are two paths for current to flow:

• I₁ is the current that goes through R1 and R2.
• I₂ is the current that flows through R3 and Rx.

Now, let’s look at what happens in the two loops of this circuit.

Loop 1: PSQP

In this loop, current I₂ flows through R3 and current I₁ flows through R1.

Using simple electrical rules, we get this equation:
–I₂ × R3 + I₁ × R1 = 0

Loop 2: RQSR

In this loop, current I₁ flows through R2 and I₂ flows through Rx.

This gives us another equation:
I₁ × R2 – I₂ × Rx = 0

Now let’s rearrange these equations to make things easier:

From the first loop:
I₂ / I₁ = R1 / R3

From the second loop:
I₂ / I₁ = R2 / Rx

Now, since both are equal to I₂ / I₁, we can set them equal to each other:

R1 / R3 = R2 / Rx

Now, we just solve this for Rx, the unknown resistance:

👉 Rx = (R2 × R3) / R1

Advantages of Wheatstone’s Bridge

The Wheatstone Bridge is a very useful and smart tool in the world of electricity. Here are some of its main advantages:

Helps Build a Meter Bridge

One of the best uses of the Wheatstone Bridge is that it helps us make a meter bridge, which is another helpful tool to measure resistance.

Accurately Measures Resistance

Its biggest advantage is that it can measure electrical resistance very accurately. And the best part? You don’t need expensive machines for this!

Detects Even Tiny Changes

It can catch very small changes in resistance, even those in the range of milliohms (mΩ). That’s super useful when you’re working with delicate or sensitive materials.

Easy to Find Unknown Resistance

If you know the value of three resistors in the bridge, finding the fourth one (the unknown resistor) becomes very easy.

Used to Measure Strain and Pressure

This bridge is not just about electricity. It can also help measure things like pressure and strain when used with special sensors.

Disadvantages of Wheatstone Bridge

While the Wheatstone Bridge is a useful tool for measuring resistance, it also has some drawbacks. Let’s look at them in a very simple way:

Sensitive to Temperature and Battery Power
The results can change if the temperature goes up or down, or if the battery (EMF cell) is not steady.

Needs a Good Galvanometer
If the galvanometer (the device that shows current) is not of good quality, the readings may not be correct.

Doesn’t Work Well When Unbalanced
The bridge only gives correct results when it is balanced. If it’s not, it doesn’t work properly.

Can’t Measure High Resistance
This bridge is not made to measure very large resistances. It only works well with small or medium values.

High Maintenance Cost
Taking care of the Wheatstone Bridge and keeping it working properly can cost a lot of money.

Wheatstone Bridge Applications

The Wheatstone Bridge is a smart and powerful tool used in science, especially in physics. It helps us measure things with great accuracy. Over time, people have also made small changes to it, which makes it even more useful in many ways. Here are some simple and clear ways we use the Wheatstone Bridge:

Measuring Resistance:
The most common and important use of the Wheatstone Bridge is to measure resistance. It does this with great precision. There is also something called a Meter Bridge, which is based on the Wheatstone Bridge. With just a few everyday tools and a galvanometer, we can find out the value of an unknown resistance.

Measuring Capacitance, Inductance, and Impedance:
By changing or modifying the basic Wheatstone Bridge a little, we can use it to measure other things like capacitance (how much charge something can store), inductance (how well something resists changes in current), and impedance (which includes both resistance and reactance in circuits). This makes it very useful in electrical and electronic work.

Measuring Physical Quantities:
The Wheatstone Bridge can also help us measure real-world things like temperature, strain (stretching or pressure on an object), and light. To do this, it is often used with something called operational amplifiers. These are small devices that make signals stronger and easier to read.

Limitations of the Wheatstone Bridge

The Wheatstone Bridge is a very smart and useful tool for measuring resistance. But like everything else, it has some drawbacks too. Let’s look at them in a very simple way:

Not Good for Measuring Very Small Resistance
When we try to measure very tiny resistances using a Wheatstone Bridge, it doesn’t work very well. That’s because the wires and the points where we connect things (called contacts) also have a little bit of resistance. This extra resistance can confuse the reading and give us a wrong result. For this kind of work, a better version called the Kelvin Double Bridge is used instead.

Not Suitable for Very High Resistance
If we try to measure very large resistances (like in the range of mega-ohms or even giga-ohms), the Wheatstone Bridge again starts giving trouble. The bridge becomes too sensitive, and even a small imbalance can make the reading jump or behave oddly. So, it’s not a good choice for measuring high resistance.

Changes in Temperature Can Affect Results
When electricity flows through a wire, it produces heat. This heat can change the resistance of the wire. So, if the wire gets too warm, the resistance will not stay the same. This can cause errors in the reading. If too much current is used, this error becomes even bigger.

FAQ