Kirchhoff Law Class 12th KCL & KVL exam useful important facts

Kirchhoff Law Class 12

Kirchhoff gave two laws to solve complex circuits, namely ;

1. Kirchhoff Current Law ( KCL )
2. Kirchhoff Voltage Law (KVL)

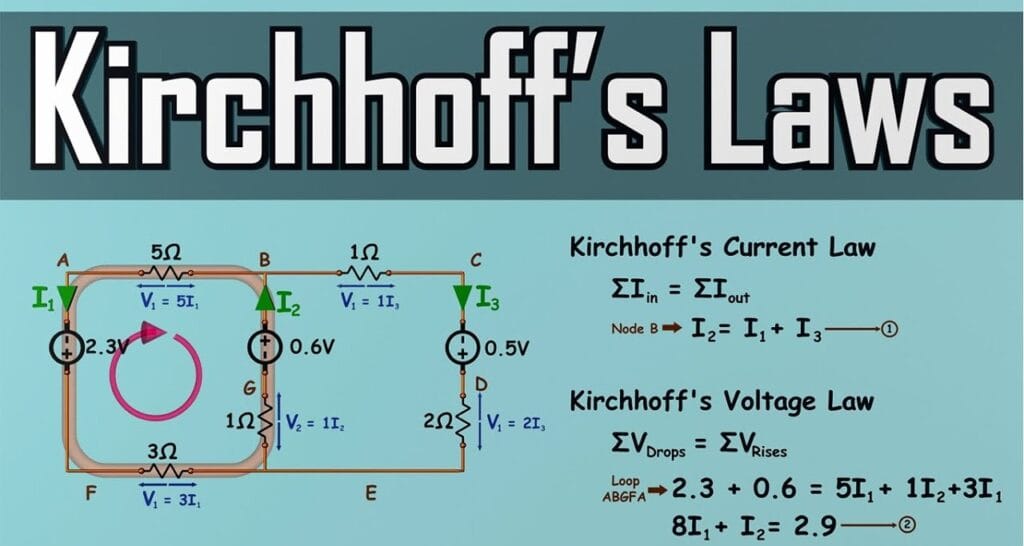
Kirchhoff Current Law ( KCL )

or Kirchhoff First Law

Kirchhoff Current Law is a basic and very important rule in electricity. It helps us understand how electric current flows in a circuit.

This law is about junctions in an electrical circuit. A junction is a point where three or more wires or branches come together.

Now, here’s what the law says:

“The total current coming into a junction is always equal to the total current going out of the junction.”

In simple words, what comes in must go out. Nothing gets lost or created at the junction.

Let’s make it even easier:

Imagine water flowing through pipes. If water comes into a point from different pipes, the same amount of water must leave that point through other pipes. The same thing happens with electric current at a junction.

We can also write this as:

The sum of all the currents at a junction is zero.

That’s because we take current going into the junction as positive, and current going out as negative (or the other way around — just be consistent). So when we add all the currents together, they cancel out and the result is zero.

Example

Let’s say there are four wires meeting at one point — call it point O.

• Current I1 goes into the junction.
• Current I2, I3, and I4 go out of the junction.

Then, according to KCL:

I1 – I2 – I3 – I4 = 0

Or we can write:

I1 = I2 + I3 + I4

This means the current coming in is equal to the total current going out.

Why It’s Important

Kirchhoff Current Law helps electricians, engineers, and students solve and understand circuits. It’s a simple rule, but it’s very powerful and always true in any electrical circuit.

In short:
Kirchhoff Current Law tells us that electric current is never lost. It just moves in and out of junctions, like traffic at a crossing — everything balances out.

Kirchhoff Current Law – Explained Simply

Let’s imagine a place in an electric circuit where wires meet — we call this a junction or point O.

Now, think of electric current like water flowing through pipes. Some water may flow into the junction, and some may flow out of it. Just like water can’t pile up at a point, electricity can’t either. The amount that flows in must be the same as the amount that flows out. This idea is the heart of Kirchhoff Current Law.

What does the law say?

The total current coming into a junction is equal to the total current going out of that junction.

We can also say:

Incoming current = Outgoing current

So, if you have different currents flowing in and out of a junction (like I₁, I₂, I₃, and I₄), you give a positive sign to the ones coming in, and a negative sign to the ones going out.

For example:

I₁ + I₄ – I₂ – I₃ = 0

This is just another way of saying that:

I₁ + I₄ = I₂ + I₃

This means the sum of incoming currents equals the sum of outgoing currents.

Why is this law true?

Because electric current is just moving electrons, and electrons can’t just stop and collect at one point. That would break the rule of nature called the law of conservation of charge, which says that charge (just like energy) cannot be created or destroyed.

So, Kirchhoff Current Law is really based on this deep truth of nature — that charge is always conserved.

In simple words:

Wherever wires meet in a circuit, the electricity that goes in must come out. Nothing gets lost, and nothing extra gets made.

That’s what makes Kirchhoff Current Law so important and so useful in understanding how electricity moves in any circuit.

Kirchhoff Voltage Law (KVL)

or Kirchhoff second Law

Kirchhoff’s Voltage Law is a simple but powerful idea used in electrical circuits. It helps us understand how voltage works in a closed loop, or a complete path, in a circuit.

Let’s say it in a very simple way:

In any closed circuit or loop, if you add up all the voltages (from batteries and resistors), the total will always be zero.

This means:

• All the energy given by the power sources (like batteries)
• Is exactly equal to
• All the energy used by the components (like bulbs or resistors)

So, if we go around a closed path in a circuit, starting and ending at the same point, the total gain and total loss of voltage will cancel each other out. There is no leftover energy and nothing is lost or created magically. Everything is balanced.

Think of it like this:
Imagine walking in a circle and coming back to the same spot. If you go uphill and then downhill, your total height difference is zero. In the same way, when electric charge goes around a closed loop and comes back to the starting point, the total energy it gains and loses is zero.

This law is based on a very important principle in physics:

The law of conservation of energy – energy cannot be created or destroyed, only changed from one form to another.

So, in electrical terms:

• The energy supplied by the battery is used up by the other components like wires, resistors, or bulbs.
• After completing the loop, the charge has used up all the energy it was given.
• That’s why the algebraic sum of all voltages in the loop is zero.

This law is also known as the loop rule.

Complex Circuits

Sometimes, we come across electrical circuits that are not easy to solve using the usual methods of series and parallel combinations. These circuits are different. They may have more than one battery or power source, or the resistors might be connected in a way that looks confusing. Because of this, we can’t use Ohm’s Law directly to solve them.

These types of circuits are called complex circuits.

Let’s look at two examples to understand this better.

Example 1: A Circuit with Two Batteries

Imagine a circuit with two batteries (we call them E₁ and E₂) and three resistors (R₁, R₂, and R₃).
Now, you might think, “Can we treat R₁ and R₃ as being in parallel?” Not really. Why? Because there’s a battery (E₁) sitting between them.
Then you might ask, “Are they in series?” Again, no. Because the same current is not passing through both of them.
So, we cannot solve this circuit by calling parts of it series or parallel. It’s just too mixed up for that.

Example 2: A Circuit with One Battery

In the second example, the circuit has only one battery but still looks complicated. The resistors here are not in neat lines like we usually see.
Resistors R₁ and R₂ are not in series — they don’t carry the same current.
They’re also not in parallel — they don’t have the same voltage across them.
This means we can’t group any of the resistors using series or parallel rules.

So, what do we do when we face such tricky circuits?
That’s where Kirchhoff Law class 12th come in. These laws, made by a scientist named Gustav Kirchhoff, help us solve complex circuits step by step — even the ones that look confusing at first glance.

In simple words:
If you can’t solve a circuit by calling parts of it “series” or “parallel,” it’s a complex circuit — and for that, we need special rules like Kirchhoff’s Laws

Sign Convention (Made Simple)

When we use Kirchhoff Voltage Law (KVL) to solve a closed electric circuit, we need to add up voltages correctly. That’s why signs (positive or negative) are very important.

Here’s an easy rule to remember:

A rise in voltage (or potential) is given a positive sign, and a drop in voltage is given a negative sign.

Let’s understand this with a battery or cell:

• If we move from the positive terminal to the negative terminal of a battery, there is a drop in voltage. So, we give it a negative sign.
• If we move from the negative terminal to the positive terminal, there is a rise in voltage. So, we give it a positive sign.

It’s really that simple!

Now, think about this:
When a charge goes all the way around a loop in a circuit and comes back to where it started, all the voltage rises and drops must cancel each other out. That’s what Kirchhoff’s Voltage Law tells us.

So, the total energy gained (from batteries or power sources) will always be equal to the total energy lost (across resistors or other components).

👉 Just remember:

• Go against the battery (negative to positive): +ve sign
• Go with the battery (positive to negative): –ve sign

Also, you can use the opposite rule too, where:

• Rise is negative
• Drop is positive

Both methods work — just stay consistent throughout the circuit.

And finally, the sign of the battery’s voltage does not depend on the direction of current in that branch. It only depends on which way you are moving across the battery while applying the law.

2. When electric current passes through a resistor, the voltage changes across it. Imagine you are walking along the resistor in the same direction the current is flowing. As you move, the voltage drops, which means the electric potential becomes lower. This is because current always flows from a higher voltage to a lower voltage. Because of this drop, we give the voltage change a negative sign.

For example, if you start at point A and move to point B along the resistor in the direction of the current, the voltage goes down. So, the voltage drop from A to B is negative.

But if you move the opposite way—against the current flow—the voltage actually rises. In this case, the voltage change is positive. So, going from A to B against the current, the voltage goes up, and we assign a positive sign to this change.

Remember, whether the voltage change is positive or negative depends on which way you are moving through the resistor compared to the current flow. It doesn’t depend on the polarity of the power source in the circuit.

Illustration of Kirchhoff Laws

Imagine you have some electric wires connected in a circuit, with batteries and bulbs. Kirchhoff’s Laws help us understand how the electric current flows through these wires.

What are Kirchhoff Laws?

There are two important rules:

1. Kirchhoff Current Law (KCL):
   At any point where wires meet (called a junction), the total current flowing into the junction is always equal to the total current flowing out. Think of it like water flowing through pipes—whatever water flows into a junction must flow out somewhere else.
2. Kirchhoff Voltage Law (KVL):
   If you walk around a closed loop in a circuit, adding up all the rises and drops in electric voltage, they will always balance out to zero. Imagine walking up and down hills in a circle — when you get back to where you started, your net change in height is zero.

How to Use Kirchhoff’s Laws in a Circuit

Let’s look at an example with a circuit having a few wires and batteries.

Current Direction:
When you guess which way the current flows, it doesn’t have to be perfect. If your guess is wrong, the answer will simply come out negative, which tells you the actual current flows the opposite way.

Current at a Junction:
Suppose two currents, I1 and I2, flow into a junction named C. The current flowing out from that junction along another wire, say CF, will be I1 + I2. This follows Kirchhoff’s Current Law.

Voltage in a Loop:
Consider a loop in the circuit marked ABCFA. There’s a battery in this loop giving voltage E1. As you go around the loop in order, from A to B to C and so on, you’ll find some places where the voltage rises (like going uphill) and places where it drops (like going downhill). For example, when you move through the battery from its negative side to its positive side, the voltage goes up, so we count that as +E1.
When you move through a resistor where the current is flowing, the voltage drops. So if the current through resistor R1 is (I1 + I2), the voltage drop is (I1 + I2) × R1, which we count as negative.

Putting it all together in the loop ABCFA:

If you add all these voltage rises and drops, they should equal zero, according to Kirchhoff’s Voltage Law. So, the equation looks like this:

−(I1+I2)×R1+E1=0 times Or simply

E1=(I1+I2)×R1

This equation tells us how the battery voltage relates to the current flowing through the resistor.

2. Putting it all together in the loop CDEFC

loop CDEFC in the circuit. As we move around this loop in that order, we observe the following:

• The voltage drop across resistor R2 (caused by current I2) is positive.
• The voltage of the battery E2 is negative in this direction.
• The voltage drop across resistor R1 (caused by the total current I1 + I2) is also positive.

Using Kirchhoff’s voltage law, which says the total sum of voltage changes around any closed loop is zero, we can write the equation for this loop as:

I2 × R2 + (I1 + I2) × R1 − E2 = 0

Rearranged, this becomes:

I2 × R2 + (I1 + I2) × R1 = E2

We already know the values of E1, E2, R1, and R2 from the circuit. So, using this equation and another one from a different loop (not shown here), we can solve for the currents I1 and I2.

Once we find these currents, we know how much current flows in every part of the circuit.

How to Solve Electrical Circuits Using Kirchhoff Laws

Guess the currents: First, pick the unknown currents flowing through the wires in the circuit. Show which way you think each current is going by drawing arrows.

Pick a loop: Choose any closed path (loop) in the circuit. Then, add up all the voltage drops (the energy used by resistors or other parts) and the voltages supplied (like batteries) around that loop.

Set the sum to zero: According to Kirchhoff’s Voltage Law, when you add up all the voltage drops and sources around the loop, the total must equal zero. So, write this as an equation.

Make enough equations: Do this for as many loops as you need to match the number of unknown currents. Each loop gives you one equation.

Solve the equations: Use the equations you wrote to find the values of the unknown currents.

Check the direction: If any current you find is negative, that means the current actually flows opposite to the direction you guessed.

impotent point

Note: Kirchhoff laws also work for circuits with alternating current (AC). The only difference is that instead of simple values for current (I), voltage (V), and resistance (R), you use special forms called phasors for current, voltage, and impedance (Z).

Example

Problem:
We have a Wheatstone bridge named ABCD with the following resistances:

• AB = 1000 ohms
• BC = 100 ohms
• CD = 450 ohms
• DA = 5000 ohms

A galvanometer with resistance 500 ohms is connected between points B and D. A 4.5-volt battery, which has negligible internal resistance, is connected between points A (positive terminal) and C. We want to find the amount of current flowing through the galvanometer and its direction.

Goal:
Find the size (magnitude) and direction of the current flowing through the galvanometer.

Solution:

Sure! Here’s a clear, simple, and easy-to-understand explanation of the Wheatstone bridge problem and its solution, written naturally as if by a human, with no complicated jargon:

shows the Wheatstone bridge ABCD. Mark the currents in the various
sections as shown. Three loops will be considered since there are three unknown quantities (viz. I1, I2 and Ig ).

Loop ABDA. Applying KVL,

−1000 I1 − 500 Ig + 5000 I2 = 0
or 2 I1 + Ig − 10 I2 = 0 …(i)

Loop BCDB. Applying KVL,

−100(I1 − Ig) + 450(I2 + Ig) + 500Ig = 0
or 2 I1 − 21 Ig − 9 I2 = 0 …(ii)

Loop EABCFE. Applying KVL,

−1000I1 − 100 ( I1 − Ig ) + 4.5 = 0
or 1100 I1 − 100 Ig = 4.5 …(iii)

Subtracting eq. (ii) from eq. (i), we get,
22 1g − I2 = 0 …(iv)
Multiplying eq. (i) by 550 and subtracting eq.
(iii) from it, we get,
650 Ig − 5500 I2 = − 4.5 …(v)

Multiplying eq. (iv) by 5500 and subtracting eq. (v) from it, we get,
120350 Ig = 4.5

120350 = 37.4 × 10–6 A = 37.4 µA from B to D

Answer:
The current flowing through the galvanometer is about 37.4 microamperes (µA), and the direction of this current is from point B to point D.

Example 2

We are given a Wheatstone bridge that looks like a square with four resistors on the sides and one resistor connecting two opposite corners.

Here’s what we know:

• Resistor AB = 1 Ω
• Resistor BC = 2 Ω
• Resistor CD = 3 Ω
• Resistor DA = 4 Ω
• A 5 Ω resistor connects point B to D (this is the diagonal resistor).
• A 4-volt battery (with 1 Ω internal resistance) is connected between points A and C.

We are asked to find:

1. The current through the 5 Ω resistor (between B and D) and its direction.
2. The total resistance between A and

Step-by-step Solution:

Let’s name the currents in the different branches:

• Current in AB is I₁
• Current in DA is I₂
• Current in BD (the 5 Ω resistor) is I₃

Now, using Kirchhoff Voltage Law (KVL), we’ll form equations by going around loops in the circuit.

First loop: ABDA

We go from A to B to D to A again.

The equation becomes:

– (1 × I₁) – (5 × I₃) + (4 × I₂) = 0
→ I₁ + 5I₃ – 4I₂ = 0 → (Equation 1)

Second loop: BCDB

We go from B to C to D to B again.

The voltage drop across each resistor gives:

– 2(I₁ – I₃) + 3(I₂ + I₃) + 5I₃ = 0
→ 2I₁ – 10I₃ – 3I₂ = 0 → (Equation 2)

Third loop: Battery loop (A to C via the battery)

Going through the battery and resistors from A to C:

–1 × I₁ – 2(I₁ – I₃) – 1(I₁ + I₂) + 4 = 0
→ 4I₁ – 2I₃ + I₂ = 4 → (Equation 3)

Now, solve the equations step-by-step:

Start with:

1. I₁ + 5I₃ – 4I₂ = 0
2. 2I₁ – 10I₃ – 3I₂ = 0
3. 4I₁ – 2I₃ + I₂ = 4

Step 1: Multiply Equation 1 by 2:

2I₁ + 10I₃ – 8I₂ = 0

Now subtract Equation 2:

(2I₁ + 10I₃ – 8I₂) – (2I₁ – 10I₃ – 3I₂) = 0
→ 20I₃ – 5I₂ = 0 → (Equation 4)

Step 2: Multiply Equation 1 by 4:

4I₁ + 20I₃ – 16I₂ = 0

Now subtract Equation 3:

(4I₁ + 20I₃ – 16I₂) – (4I₁ – 2I₃ + I₂) = 0
→ 22I₃ – 17I₂ = –4 → (Equation 5)

Now solve Equation 4 and Equation 5 together:

• From Equation 4: I₂ = 4I₃
• Put this into Equation 5:

22I₃ – 17(4I₃) = –4
→ 22I₃ – 68I₃ = –4
→ –46I₃ = –4
→ I₃ = 4 / 46 = 0.087 A

Final Answers:

(i) Current in the 5 Ω resistor (I₃):
The current is 0.087 A
It flows from point B to point D.

(ii) Resistance between A and C:

Now, calculate other currents:

• I₂ = 4 × 0.087 = 0.348 A
• Use Equation 2 to find I₁:

2I₁ – 10I₃ – 3I₂ = 0
→ 2I₁ = 10 × 0.087 + 3 × 0.348
→ 2I₁ = 0.87 + 1.044 = 1.914
→ I₁ = 0.957 A

Total current from battery = I₁ + I₂ = 0.957 + 0.348 = 1.305 A

Now, voltage drop inside battery = 1 Ω × 1.305 A = 1.305 V
So, voltage across A and C = 4 – 1.305 = 2.695 V

Now use Ohm’s Law:

Resistance between A and C = Voltage / Current
= 2.695 V / 1.305 A ≈ 2.065 Ω

Final Summary:

• ✅ Current through 5 Ω resistor = 0.087 A, from B to D
• ✅ Resistance between A and C = 2.065 Ω
  
  
  

calculation

Understanding Kirchhoff Law Class 12 with a Simple Calculation

When you study Kirchhoff Law Class 12, you will come across two very important rules – Kirchhoff Current Law and Kirchhoff Voltage Law. These laws help us understand how current and voltage behave in a circuit.

Let’s first understand Kirchhoff Current Law. According to Kirchhoff Current Law, the total current entering a junction is equal to the total current leaving the junction. This means that no current is lost at the junction.

Now let’s look at Kirchhoff Voltage Law. According to Kirchhoff Voltage Law, the total voltage around any closed loop in a circuit is zero. This means that if you go around a loop, all the energy supplied by the battery is used up by the resistors or other components in the loop.

Let’s solve a simple example using both Kirchhoff Current Law and Kirchhoff Voltage Law. This will help you understand Kirchhoff Law Class 12 in a practical way.

FAQ