Top 10 Powerful Insights into the Equivalent Circuit of a Transformer:

1. Introduction

Transformers are vital components in electrical power systems, used to step up or step down voltages efficiently. However, a real transformer is not perfect — it has losses and non-idealities. The equivalent circuit is a simplified model that represents these imperfections, helping engineers analyze and design transformers effectively.

2. What is an Equivalent Circuit?

An equivalent circuit is a simplified electrical representation of a transformer that mimics its real behavior. It models resistances, reactances, and losses so that calculations of performance, voltage regulation, and efficiency can be made accurately.

Equivalent Circuit of a Transformer

The equivalent circuit of a transformer is an electrical model that allows the prediction of transformer performance under various loading conditions without physically loading it. Performance indicators include:

• No-load current
• Iron loss
• Copper loss
• Efficiency
• Voltage regulation

The equivalent circuit of a transformer is an electrical representation that helps predict transformer performance under various loading conditions without the need for physical testing. It allows estimation of parameters like no-load current, iron loss, copper loss, efficiency, and voltage regulation.

This model is based on the current and voltage equations used to draw the phasor diagrams. By using these equations, a practical transformer can be modeled as a combination of:

• An ideal transformer
• Winding resistances
• Leakage reactances

3. Components of the Equivalent Circuit

1. Winding Resistance (R₁, R₂)
   • Represents the resistance of primary and secondary windings.
   • Causes copper loss (I²R loss) in the transformer.
2. Leakage Reactance (X₁, X₂)
   • Represents the effect of leakage flux that does not link both windings.
   • Causes voltage drops and affects voltage regulation.
3. Core Loss Resistance (R₀)
   • Connected in parallel with the magnetizing branch.
   • Represents iron loss (hysteresis and eddy current loss) in the core.
4. Magnetizing Reactance (Xₘ)
   • Also connected in parallel.
   • Represents the magnetizing current needed to produce the mutual flux in the core.
5. Load Impedance (ZL)
   • Represents the load connected to the transformer secondary.
   • Determines the output voltage and current.

No-Load Current Components

When the secondary is open, a small no-load current I₀ flows in the primary. It has two parts:

• Magnetizing Component (Iµ):
  Perpendicular to the voltage. Produces the mutual flux in the core. Represented by magnetizing reactance Xₘ.
• Working (Iron Loss) Component (Iw):
  In phase with voltage. Represents the active power consumed in the core. Represented by resistance R₀.

Mathematically: I0=Iw+jIµI₀ = Iw + jIµI0​=Iw+jIµ

4. Derivation of the Equivalent Circuit of a Transformer

Transformers are essential in electrical systems to transfer energy between circuits efficiently. However, real transformers are not ideal—they have some resistance, leakage flux, and core losses. To understand how they work under real conditions, we use an equivalent circuit.

Understanding the Basics

An ideal transformer assumes no losses and perfect magnetic coupling. But in practice, we have to account for:

• Winding resistance
• Leakage reactance
• Core loss
• Magnetizing current

These factors affect the voltage, current, and efficiency of the transformer.

Step 1: Series Impedance of Windings

Let R1 and X1 be the primary winding resistance and leakage reactance. R2 and X2 are the secondary winding resistance and leakage reactance.

The voltage drops across the windings are:

• Primary voltage: V1 = I1(R1 + jX1) + E1
• Secondary voltage: V2 = I2(R2 + jX2) + E2

Here, E1 and E2 are the induced EMFs in the primary and secondary windings.

Step 2: Referring Secondary Side to Primary Side

To simplify calculations, we refer secondary parameters to the primary side using the turns ratio a = N1 / N2:

• Referred secondary resistance: R2′ = R2 × a²
• Referred secondary reactance: X2′ = X2 × a²
• Referred secondary current: I2′ = I2 / a

The total series impedance on the primary side is:

• Zeq = R1 + jX1 + R2′ + jX2′

Step 3: Core Loss and Magnetizing Branch

The core has iron losses (hysteresis and eddy current losses) and requires a magnetizing current. These are represented by a parallel branch across the primary:

• Core loss resistance: Rc = V1² / Pcore
• Magnetizing reactance: Xm = V1 / Im

Where Pcore is the power loss in the core and Im is the magnetizing current.

Step 4: Equivalent Circuit Representation

The final equivalent circuit referred to the primary side has:

• Series branch: R1 + jX1 + R2′ + jX2′
• Parallel branch across the primary: Rc and Xm

This model helps in analyzing:

• No-load current
• Voltage regulation
• Efficiency
• Load currents and voltage drops

Key Formulas

• R2′ = R2 × a²
• X2′ = X2 × a²
• Zeq = R1 + jX1 + R2′ + jX2′
• Rc = V1² / Pcore
• Xm = V1 / Im

By using the equivalent circuit, engineers can accurately predict how a real transformer behaves and ensure it operates efficiently under various conditions.

5. Types of The Equivalent Circuit of a Transformer

Transformers are key components in electrical systems, and understanding their equivalent circuits helps engineers and students analyze their behavior. Equivalent circuits are simplified models of transformers that show the effect of real-world elements like resistance, leakage, and core losses.

1. Referred to Primary Side

In this type, all secondary side parameters are converted to the primary side using the turns ratio a = N1 / N2. This makes it easier to calculate voltages, currents, and losses from the primary side view.

• Referred secondary resistance: R2′ = R2 × a²
• Referred secondary reactance: X2′ = X2 × a²
• Referred secondary current: I2′ = I2 / a

The total series impedance on the primary side is:

Zeq = R1 + jX1 + R2′ + jX2′

2. Referred to Secondary Side

Here, all primary side parameters are converted to the secondary side. This approach is useful when analyzing from the load or secondary point of view.

• Referred primary resistance: R1′ = R1 / a²
• Referred primary reactance: X1′ = X1 / a²
• Referred primary current: I1′ = I1 × a

The total series impedance on the secondary side is:

Zeq = R1′ + jX1′ + R2 + jX2

3. Approximate Equivalent Circuits

Approximate equivalent circuits are simplified models for quick calculations. They ignore small elements like magnetizing current or core losses, which have minimal impact under load conditions. These are often used for estimating voltage drops, efficiency, and load current quickly.

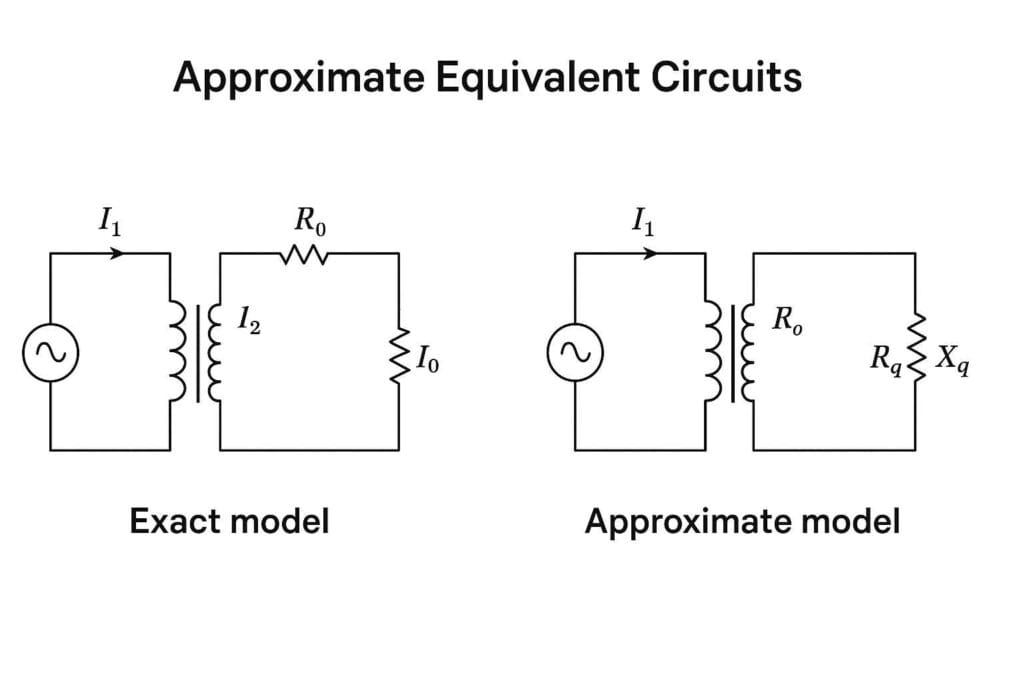
Benefits of Approximate Circuits

• Easier and faster calculations
• Good enough for many practical purposes
• Helps students understand basic transformer behavior without complex math

6. Significance of the Equivalent Circuit of a Transformer

The equivalent circuit of a transformer is a crucial tool for understanding and predicting the transformer’s behavior. By using this simplified model, engineers and students can calculate important performance parameters without testing the actual transformer under real conditions.

1. Calculating Voltage Regulation

Voltage regulation tells us how much the voltage drops when the transformer is under load compared to when it is not loaded. Using the equivalent circuit, voltage drops due to winding resistance and leakage reactance can be calculated easily.

Voltage Regulation (%) = ((V_no-load – V_full-load) / V_full-load) × 100

This helps in designing transformers to maintain a stable voltage under varying loads.

2. Predicting Efficiency

Efficiency shows how much of the input power is effectively transferred to the output. The equivalent circuit allows us to calculate copper losses (in the windings) and core losses (in the magnetic core) to predict transformer efficiency.

Efficiency (%) = (Output Power / Input Power) × 100

By analyzing the equivalent circuit, we can identify ways to improve efficiency by reducing losses.

3. Performing Fault and Load Analysis

The equivalent circuit helps engineers analyze how transformers behave under different loading conditions and during faults. By using series and parallel components representing resistance, reactance, and core characteristics, it becomes possible to:

• Determine currents under short-circuit or overload conditions.
• Estimate the effect of load changes on secondary voltage.
• Plan protective devices and maintenance schedules.

7. Simplification of the Equivalent Circuit of a Transformer

Transformers are essential devices in electrical systems, and understanding their equivalent circuit helps in analyzing performance. The complete equivalent circuit has parameters on both the primary and secondary sides, which can make calculations complex. To simplify, we can refer all parameters to one side—usually the primary.

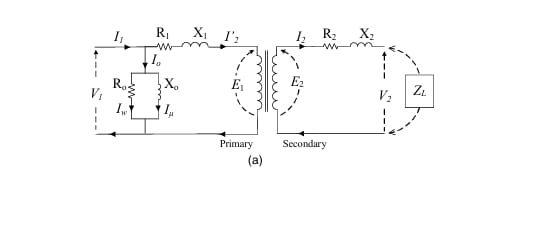
1. Simplifying by Referring to the Primary Side

Step 1: Shift the No-Load Branch

The no-load branch, which consists of the parallel combination of Rc and Xm, can be shifted toward the source side with minimal loss of accuracy. This branch is also called the exciting branch. The new arrangement shows the no-load branch at the primary side, making further analysis easier.

Step 2: Refer Secondary Parameters to Primary Side

The secondary winding resistance R2 and leakage reactance X2 can be referred to the primary side as R2′ and X2′ respectively using the turns ratio a = N1/N2:

• R2′ = R2 × a²
• X2′ = X2 × a²

Now, the primary and referred secondary resistances and reactances are in series:

• Total series resistance: Req = R1 + R2′
• Total series leakage reactance: Xeq = X1 + X2′

Step 3: Connect Load Impedance

The load impedance ZL can now be connected across the secondary, but all calculations can be performed using the primary-referred equivalent circuit.

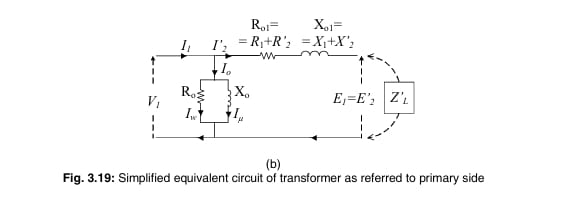
Formulas for Simplified Equivalent Circuit

• Equivalent resistance referred to primary side: Req = R1 + R2′
• Equivalent leakage reactance referred to primary side: Xeq = X1 + X2′
• Equivalent impedance referred to primary side: Zeq = Req + jXeq

2. Referring the Equivalent Circuit to the Secondary Side

When we move all the ohmic elements from the primary side to the secondary side, we get the following values:

• No-load resistance referred to secondary side: R0′ = K × R0
• Magnetizing reactance referred to secondary side: Xm’ = K × Xm
• Resistance of primary winding referred to secondary side: R1′ = K × R1
• Leakage reactance of primary winding referred to secondary side: X1′ = K × X1

Where K = (N2/N1)², the square of the turns ratio.

Equivalent Resistance and Reactance

• Equivalent resistance of complete transformer referred to secondary side: Req’ = R2 + R1′ = R2 + K × R1
• Equivalent leakage reactance of complete transformer referred to secondary side: Xeq’ = X2 + X1′ = X2 + K × X1

Equivalent Impedance

The total equivalent impedance referred to the secondary side is then:

Zeq’ = Req’ + jXeq’ = (R2 + K × R1) + j(X2 + K × X1)

Benefits of Simplification

• Simplifies calculations for load conditions.
• Easier to compute voltage drop, current, and efficiency.
• Makes transformer design and analysis more straightforward.

8. Practical Applications of the Equivalent Circuit of a Transformer

Understanding the equivalent circuit of a transformer is very useful in real-world applications. It helps engineers and technicians design, test, and improve transformers efficiently. Here are some practical uses:

1. Transformer Design Optimization

By using the equivalent circuit, engineers can plan the transformer design to meet specific requirements:

• Determine the right wire sizes to handle current without overheating.
• Choose the correct core material to reduce core losses.
• Adjust winding turns to get the desired voltage ratio.

2. Performance Prediction Before Manufacturing

The equivalent circuit allows performance predictions without building the transformer:

• Calculate No-load current and Voltage regulation using the formulas:
  • Zeq = R1 + jX1 + R2′ + jX2′
  • R2′ = R2 × a²
  • X2′ = X2 × a²
• Estimate Efficiency by including series and parallel branch effects.
• Predict voltage drops under different load conditions.

3. Identifying Causes of Inefficiency and Losses

Engineers can locate sources of losses and inefficiency in a transformer:

• Copper losses in series resistance: I1² × R1, I2’² × R2′
• Core losses in parallel branch: V1² / Rc
• Leakage effects that cause voltage drops: jX1, jX2′

9. Common Mistakes in Equivalent Circuit of a Transformer

When using transformer equivalent circuits, engineers and students sometimes make mistakes that can lead to incorrect calculations and poor design decisions. Here are some common errors and how to avoid them.

1. Ignoring Core Losses

Core losses, caused by hysteresis and eddy currents in the transformer core, are important to include in calculations. Ignoring them can lead to overestimating efficiency and underestimating voltage drops.

• Core loss resistance: Rc = V1² / Pcore
• Magnetizing reactance: Xm = V1 / Im

Always include the parallel branch with Rc and Xm when analyzing no-load conditions or calculating efficiency.

2. Misinterpreting Referred Parameters and Turns Ratio

Sometimes, secondary parameters are used incorrectly without referring them to the primary side. The turns ratio a = N1 / N2 is essential to convert secondary resistance, reactance, and current to the primary side.

• Referred secondary resistance: R2′ = R2 × a²
• Referred secondary reactance: X2′ = X2 × a²
• Referred secondary current: I2′ = I2 / a

Always remember to adjust all secondary parameters before combining with primary values for series calculations.

3. Overlooking Leakage Reactance Effects

Leakage reactance affects voltage regulation, especially under load. If ignored, the voltage drop across the transformer will be miscalculated, leading to inaccurate predictions of output voltage.

• Total series impedance: Zeq = R1 + jX1 + R2′ + jX2′

Include leakage reactances X1 and X2′ in series when calculating voltage drops and regulation.

10. Conclusion

Understanding and properly using transformer equivalent circuits is critical. Avoiding these common mistakes—ignoring core losses, misinterpreting referred parameters, and overlooking leakage reactance—ensures accurate analysis and better transformer performance.

FAQ