Table of Contents
relation between electric field and potential
What is an Electric Field?
Imagine a charged object, like a balloon rubbed on your hair. Around it, something invisible forms — a kind of invisible space where other charges can feel a push or a pull.
That invisible space is called an electric field.
It’s like the area around a magnet where things get pulled. But instead of magnets and metal, this is about electric charges — like positive and negative charges.
An electric field shows us how a charge affects the space around it.
Now, let’s make it even simpler:
If you place a tiny positive charge anywhere near another charge, and it feels a force — that force is because of the electric field in that space.
The electric field tells us how strong the force is, and which direction
relation between electric field and potential
Electric fields are made by electric charges. If something has charge, it creates an electric field around it.
Electric fields have strength (how strong they are) and direction (where they push).
The direction is always the way a tiny positive charge would move in that space.
We measure the strength of an electric field in volts per meter (V/m).
You can even draw electric fields using lines — we call them electric field lines. They show us the path a positive charge would take.
In short:
An electric field is like an invisible force zone around a charge. It tells us where a charge will feel a push and how strong that push will be.
What are Electric Field Lines?
Imagine you are trying to show the path that electricity would take through space. Electric field lines are like invisible threads that help us see and understand this path.
These lines don’t actually exist in real life—they’re imaginary, but very helpful. They show us two things:
Direction – which way a tiny positive charge would move if we placed it there.
Strength – how strong the electric force is in a certain area. If the lines are close together, the field is strong. If they’re far apart, the field is weak.
So, more lines in one area means more force in that space.
Where Do We Use Electric Fields?
Electric fields may be invisible, but they’re powerful and useful. We use them in many everyday and scientific devices:
Electric motors and generators – They help machines run and create electricity.
Capacitors – These are used to store energy in electronic circuits.
Batteries – The electric field moves the charge from one end to the other.
Electromagnets – Used in cranes, speakers, and even MRI machines.
Particle accelerators – Help scientists study the smallest parts of matter.
Medical imaging – Electric fields are used in many machines that scan and help treat the human body.
So, electric fields are not just a science topic—they are part of how the modern world works.
What is Electric Potential?
Electric potential is like the energy level at a certain point. If electric field is the push, then electric potential is the pressure that causes the push.
It tells us how much energy a single charge would have at a specific point in space. The higher the potential, the more energy is stored at that point.
Here are the key things to know:
- It’s called “potential” because it shows the possibility of doing work (like moving a charge).
- It’s measured in volts (V).
- It doesn’t have a direction—it’s just a number (we call this a scalar).
- The farther you move from the source of the charge, the lower the potential becomes.
- The difference in potential between two points is what makes charges move. This is also known as voltage.
In simple words:
Electric potential tells us how much push is available, and electric field tells us how hard it will push.
In Short:
Electric field lines help us see the direction and strength of electric force.
Electric fields are caused by charges and are used in many machines and tools.
Electric potential shows how much energy a charge could have at a point.
Charges move when there’s a difference in potential, and that movement is guided by the electric field.
Applications of Electric Potential
Electric potential is a very important idea in electricity. It helps us understand how charges move, how energy flows, and how electric things work around us. Here are some simple and clear ways we use electric potential:
1. To Find the Electric Field
Electric potential helps us figure out where and how strong the electric field is at any point. If we know how the potential changes from one place to another, we can find the electric field easily.
2. In Electrical Circuits
Electric potential is what we usually call voltage. It’s the reason why electricity moves in a wire. It helps engineers and scientists design things like batteries, lights, switches, resistors, capacitors, and coils. Every part in a circuit depends on the right voltage to work properly.
3. To Study Moving Charges
Charged particles, like electrons, are always trying to move from higher potential to lower potential. By knowing the electric potential, we can predict how these particles will move inside machines, wires, or even in the air.
4. In Electrochemistry
Electric potential plays a big role in chemistry too. It helps us study batteries, chemical reactions, and how electricity is produced or used in chemical processes.
5. To Understand Charges in Space
Electric potential helps us see how charges are spread out and how they affect each other. This is useful in electrostatics, where we study still (non-moving) charges and their effects.
In Simple Words:
Electric potential tells us how much energy a charge has at a certain point. It’s like the height of a hill—charges roll from high potential to low potential just like a ball rolls downhill.
It is measured in volts and depends on two things:
- How much charge there is
- How far you are from that charge
We use this idea in many fields like electricity, electronics, engineering, chemistry, and physics. Without understanding electric potential, we wouldn’t be able to build circuits, power devices, or study electric energy.
Electric Field and Electric Potential
An electric field is like an invisible force that can push electric charges. But this force doesn’t just appear on its own.
It only exists when there is a difference in electric potential between two points.
Imagine this:
You have a ball on a flat surface. It stays still. But if you place the ball on a slope, it starts rolling. Why? Because there’s a height difference. The slope gives it a push.
The same idea works in electricity.
If the electric potential (you can think of it like electric “height”) is the same everywhere, nothing moves. No electric field is created.
But the moment there’s a change—a higher point and a lower point in potential—the electric field is born. It shows up to move charges from the higher potential to the lower one.
In simple words:
Electric field is the change in electric potential over distance.
This relationship is written in math as:
E=−dV/dx
Let’s break this down:
- E stands for the electric field (the invisible force).
- V is the electric potential (like the electric “height”).
- dx is a small distance you move in space.
- The minus sign means the electric field always pushes from a place with more potential to a place with less.
In the end, no potential difference, no electric field.
Even if the potential is high, if it’s the same everywhere, nothing happens.
But when the potential changes across space, the electric field is ready to move things.
That’s the natural link between electric field and electric potential—simple, clear, and powerful.
Direction of Electric Field
The direction of the electric field simply tells us which way a tiny positive charge would move if we placed it near another charge.
- If the electric field moves from a low potential to a high potential, we say the direction is positive.
- If it moves from a high potential to a low potential, we say the direction is negative.
It’s like walking up or down a hill:
- Going uphill (from low to high) is positive.
- Going downhill (from high to low) is negative.
relation between electric field and potential
To understand this better, imagine placing a test charge (a tiny positive charge) in an electric field. The way this charge moves helps us see how the electric field and electric potential are related.
Important Ideas:
- Electric Field shows the direction and strength of the force on the test charge.
- Electric Potential tells us how much energy the test charge would have at a certain point.
Electric Potential Formula:
E=−dV/dx
This means:
The electric field is the change in electric potential across a small distance.
The negative sign shows the field points from higher potential to lower potential.
Electric Gradient
Think of the electric gradient as how “steep” the electric hill is.
Positive Gradient: As you move closer to the test charge, the potential becomes higher.
Negative Gradient: As you move away from the test charge, the potential becomes lower.
Just like with hills:
Closer = steeper and stronger.
Farther = flatter and weaker.
Equipotential Surface
This is an invisible surface where the electric potential is the same everywhere.
- On this surface, a charge doesn’t gain or lose energy.
- The electric field lines always cross these surfaces at right angles (they are perpendicular).
Imagine standing on a flat floor—it doesn’t matter where you stand, you’re at the same height. That’s what an equipotential surface is like, but for electric potential.
Simple Example
Let’s imagine something easy.
Suppose you have a tiny positive charge sitting right at the center of a space. Think of it like a glowing ball that gives off an invisible force. This force is what we call the electric field. But before we talk about that, let’s understand electric potential first.
What is Electric Potential?
Electric potential tells us how much push or energy a charge would feel if it were placed at a certain point in space. The closer you are to the glowing ball (the charge), the stronger this push or energy is.
There’s a simple formula to know the electric potential at a distance from the charge: V=k⋅q/r
- V is the electric potential
- k is a constant number (you don’t have to remember it)
- q is the amount of the charge
- r is the distance from the charge
So, as you move farther away, the value of V gets smaller. That means the electric potential drops slowly as distance increases.
What is the Electric Field?
Now, electric field is a little different. It tells us how strong the force is at any point around the charge. This is the actual “push” a charge would feel.
The formula looks like this: E=k⋅q/r2
- E is the electric field
- Everything else is the same as before
- But here, you divide by r squared, which means the electric field drops faster as you move away
So:
The electric potential gets smaller slowly with distance
The electric field gets weaker more quickly with distance
Understand the Difference
Think of a hill:
- The height of the hill at different points is like electric potential
- The steepness or slope of the hill is like the electric field
If the hill is flat (same height everywhere), you don’t feel any pull — just like no electric field.
But if the hill has a slope, you’ll feel pulled downward — that’s your electric field acting.
The Link Between Them
Here’s the key idea:
The electric field always points in the direction where the electric potential is getting lower.
Or simply:
Electric field flows from high potential to low potential — just like water flows downhill.
Difference Between Electric Field and Electric Potential
Let’s imagine you’re holding a balloon filled with electric charge. This balloon doesn’t just sit quietly—it creates an invisible area around it where it can push or pull other charges. That invisible area is called the electric field.
Now, let’s break this down in a simple way:
What is Electric Field?
The electric field is the space around a charged object where other charges can feel a push or pull.
It has both strength and direction—which makes it a vector.
We measure it in volts per meter (V/m).
The direction of the field is the way a positive charge would move if placed in that space.
You can think of the electric field like the wind—it pushes things in a certain direction with a certain force.
What is Electric Potential?
The electric potential tells us how much energy a charge would have at a certain point.
It only has magnitude, not direction—so it’s a scalar.
It is measured in volts (V).
It tells us how much work is needed to bring a positive charge from far away (infinity) to that point.
You can think of electric potential like the height of a hill—the higher you are, the more energy you have, and the more work it would take to climb up.
Differences at a Glance:
| Feature | Electric Field | Electric Potential |
|---|---|---|
| Type | Vector (has direction) | Scalar (no direction) |
| What it does | Pushes or pulls charges | Measures stored energy per charge |
| Measured in | Volts per meter (V/m) | Volts (V) |
| Created by | Charged particles | Result of electric fields |
| Direction | Points where a positive charge would move | No specific direction, just value |
Simple Words:
Electric field shows how strongly and in which direction a charge would be pushed.
Electric potential shows how much energy a charge would have in that place.
How Are They Connected?
They are tied together by a very important idea:
The electric field is the negative rate of change of electric potential with respect to distance.
Or simply: E=−dV/dx
This means the electric field points in the direction where the potential drops the fastest—just like water flowing downhill.
Electric Potential and Electric Field
Imagine you have an electric field—something like an invisible force that exists in space, created by electric charges. Now, if you take a small electric charge and slowly move it through this field, something interesting happens: its electric potential energy changes.
Let’s break this down step by step.
Suppose you have a tiny charge, let’s call it q, and you move it a very small distance along a straight path—say along the x-axis. During this movement, the electric potential (which is like a kind of electric “height” or level of energy at a point) changes a little. Let’s call that small change in potential dV.
When this happens, the change in the charge’s electric potential energy is simply:
Change in energy = charge × change in potential
or
dP = q × dV
This tells us how much energy the charge gains or loses just because it moved to a different spot in the electric field.
But there’s more. As you move the charge, you’re doing work against the electric field—just like how you’d use effort to push a ball uphill. The amount of work done depends on the strength of the electric field and the direction you’re moving the charge.
The work you do to move the charge is given by:
Work = -q × E × dx × cos(θ)
Here:
- E is the strength of the electric field.
- dx is how far you move the charge.
- θ is the angle between the direction of the field and the direction you moved.
- The minus sign shows that the field does work against you when you go in the opposite direction.
Now, E × cos(θ) just gives us the part of the electric field that points in the same direction as your movement. That’s called the x-component of the electric field, or Eₓ.
So the work you do becomes:
Work = -q × Eₓ × dx
Because energy can’t be created or destroyed—just changed from one form to another—the change in potential energy must equal the work done:
q × dV = -q × Eₓ × dx
If you cancel q from both sides (as long as it’s not zero), you get a very important relationship:
dV/dx = -Eₓ
This equation tells us something powerful:
The electric field is the rate at which electric potential changes with distance.
We show this with a simple formula:
Ex=−dVdx
This means:
The electric field in the x-direction is equal to the negative rate of change of electric potential (V) with respect to x. The minus sign tells us the electric field points in the direction where the potential decreases—just like water flows downhill, electricity “flows” from high potential to low.
What about units?
Electric potential is measured in volts (V), and distance is in meters (m). So when you divide volts by meters, you get the unit for electric field:
1 volt per meter (V/m)=1 newton per coulomb (N/C)
Both mean the same thing: how much force is felt by a 1-coulomb charge.
Let’s look at an easy example. Imagine two large flat plates, one positively charged and one negatively charged, placed apart from each other. The electric field between them is uniform, meaning it stays the same from one spot to another (like walking up a hill that never changes steepness).
In this case, the potential doesn’t jump suddenly; it changes steadily as you move. The formula becomes:
V(x)=V0−Ex⋅x
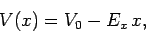
When we talk about electric potential, there’s one important thing to remember: it changes as you move through an electric field. Imagine electric potential like a kind of “height” in electricity. Just like how a ball rolls downhill due to gravity, a positive charge moves “downhill” in electric potential—it naturally wants to go from a higher potential to a lower one.
Now, there’s a special number we call V0, which is just a starting point or reference. It doesn’t change the way things move; it just helps us measure the potential more easily.
So, here’s what happens:
- A positive charge moves in the direction where the electric potential is getting smaller.
- A negative charge, on the other hand, does the opposite—it moves toward where the potential is getting higher.
This is very similar to how objects move in a gravitational field. Just like gravity pulls things downward, an electric field “pulls” charges in a certain direction.
Now, let’s talk about the electric field itself. Think of it as a kind of force map that tells charges where to go. The electric field at a point is related to how quickly the electric potential is changing at that point.
If we look at how the potential changes in different directions—left to right (x), up and down (y), and forward and back (z)—we can find the electric field using this rule:
E=−(dV/dx)
Imagine two points, A and B, very close to each other. To get from A to B, you move a little bit in the x direction, then a little bit in the y direction, and finally a little bit in the z direction. The total change in electric potential when you move from A to B is just the sum of the changes along each step.
dV=dxV+dyV+dzV.
From physics, we know that each of these small changes relates to the electric field in that direction. For example, the change along x is
−Ex dx
where
Ex is the electric field along the x-axis and
dx is the small distance moved in that direction.
Putting this together for all three directions gives us:
dV=−Ex dx−Ey dy
This can be written in a shorter, neater way using vectors as:
dV=−E⋅dr=−E dr cosθ
where E is the electric field vector, dr is the displacement vector from A to B, and θ is the angle between them.
In simple terms, the change in electric potential depends on how far you move and how strong the electric field is in the direction you move.
Common formulas
1. Infinite Wire
Imagine a wire that goes on forever and has charge spread evenly along its length.

- The electric potential near it is:
V = – (λ / 2πε₀) × ln(x) - λ is how much charge is packed per unit length.
- x is the distance from the wire.
As you move away, the potential drops slowly.
2. Infinitely Large Surface
This is like a never-ending sheet with charge spread out evenly.
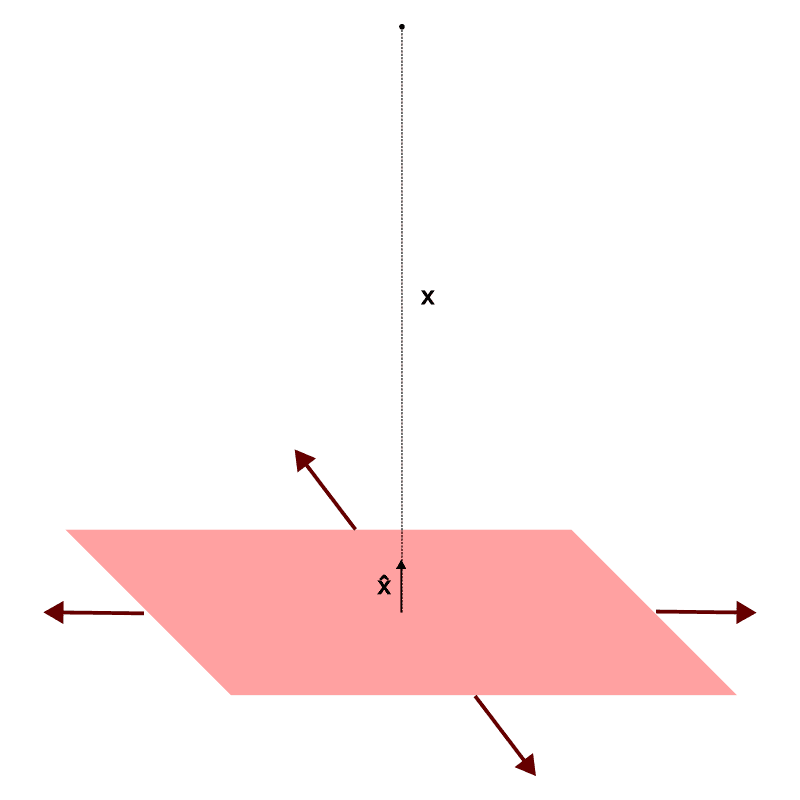
- The potential at a distance x is:
V = – (σx / 2ε₀) - σ tells how much charge is on each square unit of the surface.
Here, potential changes in a straight line as you move away.
3. Infinitely Long Cylinder (Uniformly Charged Volume)
This is like a thick wire with charge spread inside it, not just on the surface.
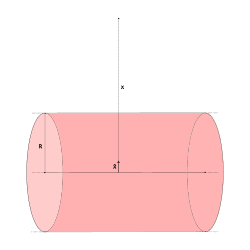
- The potential outside it is:
V = – (λ / 2πε₀) × ln(x) - λ is the charge per unit length.
Same as the wire, but thicker. The potential drops in a similar way.
4. Uniformly Charged Sphere (Volume Charge)
This is a ball where the charge is spread throughout the inside.

- Outside the sphere (distance x from center):
V = Q / (4πε₀x) - Inside the sphere (at a point r from center):
V = Q(3R² – r²) / (8πε₀R³)
Here, Q is the total charge, and R is the radius of the sphere.
The potential is smooth and continuous from inside to outside.
5. Spherical Surface (Shell of Charge)
All the charge is on the surface of a sphere.
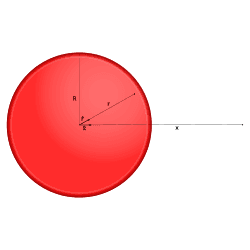
- Outside the shell:
V = Q / (4πε₀x) - Inside the shell:
V = Q / (4πε₀R)
Inside, the potential is constant — no change at all.
6. Charged Ring
This is a ring of charge, like a loop, and you’re looking at potential along its central line.
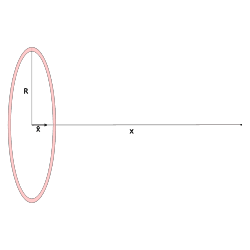
- On the axis:
V = Q / [4πε₀ √(R² + x²)]
It depends on both the radius R and the distance x from the center.
7. Charged Disc
This is like a flat round plate with charge spread out evenly.

- On the axis:
V = (σ / 2ε₀) × [√(x² + R²) – x]
The potential decreases as you move away from the center along the axis.
8. Electric Dipole
This is a pair of equal and opposite charges placed close together.
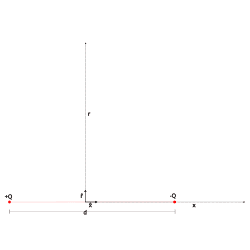
- On the equatorial line (middle line between the two charges):
V = 0 - On the axis (line connecting the two charges):
V = p / (4πε₀x²)
Here, p is the strength of the dipole, and x is your distance from the center.
FAQ
I am an Electrical Engineer with qualifications in ITI, Diploma, and B.Tech. I have worked as an ITI college instructor for 3 years and have over 5 years of hands-on experience in the electrical field. The information shared on this website is based on trusted electrical engineering textbooks such as P.S. Bimbhra, B.L. Theraja, V.K. Mehta, and real-world practical experience.