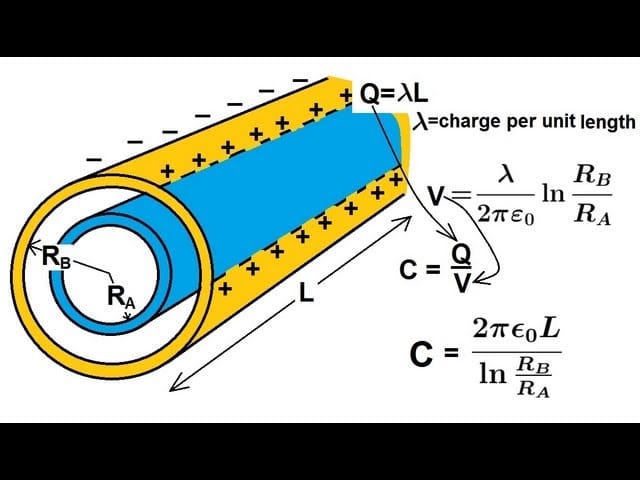
Cylindrical Capacitor
A Cylindrical Capacitor consists of two concentric conducting cylinders separated by an insulating dielectric material.
The formula gives its capacitance (C):
C = (2π ε₀ εᵣ L) / ln(b/a)
where:
- a = radius of inner cylinder
- b = radius of outer cylinder
- L = length of cylinders
- ε₀ = permittivity of free space
- εᵣ = relative permittivity of dielectric
This type of capacitor is widely used in underground and coaxial cables, where the cylindrical geometry provides uniform electric field distribution and efficient insulation performance.
Table of Contents
Introduction: What is a Cylindrical Capacitor?
A cylindrical capacitor is an electrical component made up of two round hollow conductors (cylinders) — one placed inside the other. The space between them is filled with an insulating material called a dielectric, which prevents electric current from flowing directly between the two cylinders.
- The inner tube is called the inner cylinder.
- The outer tube is called the outer cylinder.
- The dielectric between them safely stores electric energy.
In simple words, a cylindrical capacitor works just like a parallel-plate capacitor, but instead of flat plates, it has curved cylindrical surfaces that hold charge efficiently.
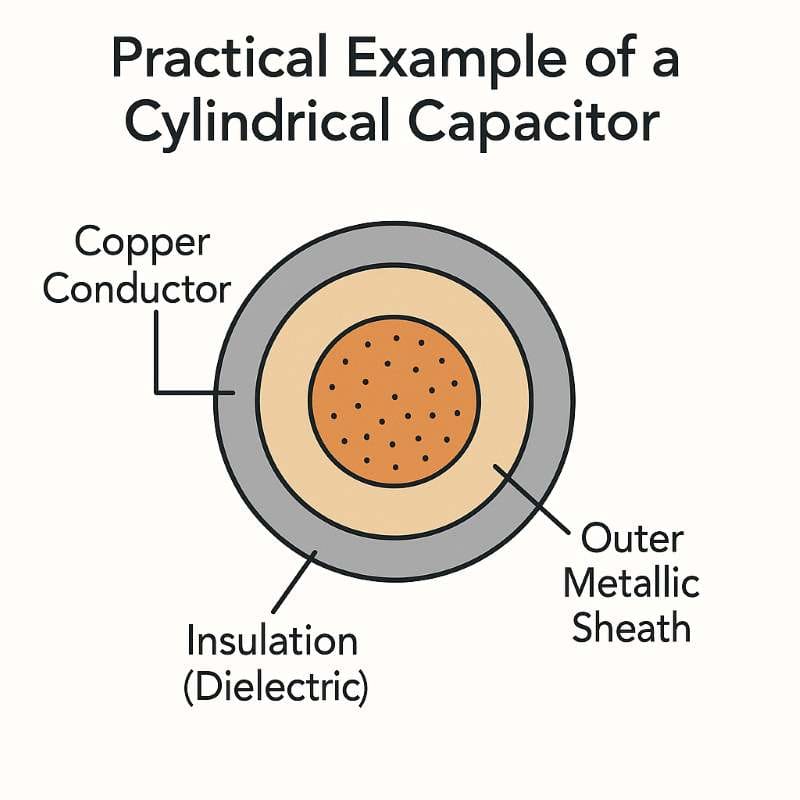
Real-Life Example of Cylindrical Capacitor – Single-Core Cable Explained
A single-core cable is a practical and common example of a cylindrical capacitor:
- The core wire inside the cable → acts as the inner cylinder.
- The outer metallic sheath → acts as the outer cylinder.
- The insulating layer between them → serves as the dielectric.
The outer sheath is usually connected to earth (ground) for safety. This design ensures smooth current flow through the inner conductor, preventing leakage or electric shocks.
Hence, a cylindrical capacitor helps safely store and manage electric energy in underground power cables and transmission systems.
⚙️ Capacitance of a Single-Core Cable
Let’s derive how to calculate the capacitance per meter of a single-core cable.
Given:
- Diameter of inner conductor = d meters
- Diameter of outer sheath = D meters
- Relative permittivity (dielectric constant) = εᵣ
- Charge per meter length = Q coulombs
Now, consider an imaginary cylindrical surface of radius x meters between the conductor and the sheath.
🔹 Step 1: Using Gauss’s Law
According to Gauss’s Law, the total electric flux through the cylindrical surface equals the charge enclosed.
Electric flux density (Dₓ) = Q / (2πx)
Unit: C/m²
🔹 Step 2: Electric Field Strength
The electric field intensity (Eₓ) at a distance x from the center is:
Eₓ = Q / (2πε₀εᵣx)
Unit: V/m
Where:
- ε₀ = Permittivity of free space = 8.854 × 10⁻¹² F/m
- εᵣ = Relative permittivity of the dielectric material
🔹 Step 3: Potential Difference Between Conductors
The voltage (V) between the inner conductor and the outer sheath is obtained by integrating the electric field between the two surfaces:
V = (Q / 2πε₀εᵣ) × log(D/d)
Unit: Volts
This represents the potential difference between the inner and outer cylinders.
🔹 Step 4: Capacitance per Meter
Capacitance is the ratio of charge to potential difference:
C = Q / V = (2πε₀εᵣ) / log(D/d)
Unit: F/m
This gives the capacitance per meter length of the cable.
🔹 Step 5: Formula
By substituting constants, the expression becomes:
C = 2.8854 × 10⁻¹¹ × εᵣ / log₁₀(D/d)
Unit: F/m
If the cable has a total length of l meters, then the overall capacitance is:
C = (2.8854 × 10⁻¹¹ × εᵣ × l) / log₁₀(D/d)
Unit: F
Or in a more practical numerical form:
C = 414 × εᵣ × l / log₁₀(D/d)
Unit: pF
Derivation of Cylindrical Capacitor Formula
Let’s define the main quantities:
- Radius of inner cylinder = a
- Radius of outer cylinder = b, where b > a
- Length of both cylinders = L
- Charge on inner cylinder = +Q
- Charge on outer cylinder = −Q
We will find the capacitance (C) of this arrangement, which measures how much charge can be stored per unit voltage.

⚙️ Step 2: Finding the Electric Field (E) Using Gauss’s Law
To determine the electric field between the cylinders, we apply Gauss’s Law.
Imagine a Gaussian cylindrical surface of radius r and length L, where a < r < b.
According to Gauss’s Law:
Electric Flux (Φ) = Charge Enclosed / Permittivity of Free Space (ε₀)
The surface area of the Gaussian cylinder = 2πrL
Therefore,
Φ = E × (2πrL) = Q / ε₀
From this, the electric field (E) is:
E = Q / (2π ε₀ r L)
This represents the electric field strength between the two cylindrical surfaces.
⚡ Step 3: Finding the Potential Difference (V)
The potential difference (V) between the inner and outer cylinders can be obtained by integrating the electric field.
We know that:
V = −∫ E dr
Substitute the expression for E:
V = −∫[a to b] (Q / 2π ε₀ r L) dr
Taking constants outside the integral:
V = −(Q / 2π ε₀ L) ∫[a to b] (1/r) dr
Integrating gives:
V = −(Q / 2π ε₀ L) [ln(b) − ln(a)]
Simplify:
V = −(Q / 2π ε₀ L) ln(b/a)
We take the magnitude (since potential decreases from inner to outer surface):
V = (Q / 2π ε₀ L) ln(b/a)
📘 Step 4: Deriving the Capacitance Formula
The general definition of capacitance is:
C = Q / V
Substitute the value of V:
C = Q / [(Q / 2π ε₀ L) ln(b/a)]
Cancel out Q from numerator and denominator:
C = (2π ε₀ L) / ln(b/a)
✅ Final Cylindrical capacitor formula
Hence, the capacitance of a cylindrical capacitor is given by:
C = (2π ε₀ L) / ln(b/a)
(Unit: Farads)
If the space between the cylinders is filled with a dielectric material of relative permittivity (εᵣ), the formula becomes:
C = (2π ε₀ εᵣ L) / ln(b/a)
🧠 Physical Meaning and Key Insights
This formula shows how the capacitance depends on:
- Length (L): Longer cylinders have higher capacitance.
- Radii (a, b): Smaller distance between cylinders increases capacitance.
- Dielectric constant (εᵣ): Higher εᵣ increases the ability to store charge.
Thus, the geometry and material between the cylinders play a vital role in determining the overall capacitance.
Factors Affecting the Capacitance of a Cylindrical Capacitor
The capacitance of a cylindrical capacitor depends on several physical dimensions and material properties. Each factor influences how much electric charge the capacitor can store per unit voltage. Let’s explore these factors in detail:
| Factor | Effect on Capacitance (C) |
|---|---|
| 1. Length (L) | Capacitance increases with an increase in the length of the cylinder. A longer cylinder offers a greater surface area for storing charge, which enhances the total capacitance. |
| 2. Dielectric Constant (εᵣ) | A higher dielectric constant allows the material to store more electric energy. Hence, using materials like mica, oil, or plastic (which have higher εᵣ values) increases the capacitance. |
| 3. Radius Ratio (b/a) | The ratio of outer to inner radius determines the distance between the cylinders. A smaller gap (lower b/a ratio) increases capacitance, while a wider gap reduces it. |
| 4. Type of Medium | Different insulating materials (air, mica, oil, plastic, etc.) have different dielectric constants (εᵣ). Replacing air with a material of higher εᵣ significantly increases capacitance. |
- Longer length → higher capacitance
- Higher dielectric constant → greater charge storage
- Smaller gap between cylinders → higher capacitance
- Better dielectric medium → improved performance
Numerical Example (Exam-Friendly)
Given:
- Inner radius, a = 1 cm = 0.01 m
- Outer radius, b = 2 cm = 0.02 m
- Length, L = 50 cm = 0.5 m
- Relative permittivity, εᵣ = 2.5
To Find: Capacitance (C)
Step 1: Formula
The formula for capacitance of a cylindrical capacitor is:
C = (2π ε₀ εᵣ L) / ln(b/a)
Where:
ε₀ = 8.854 × 10⁻¹² F/m
Step 2: Substitute the Values
C = (2π × 8.854 × 10⁻¹² × 2.5 × 0.5) / ln(2 / 1)
ln(2) = 0.693
So,
C = (2π × 8.854 × 10⁻¹² × 1.25) / 0.693
C = 1.0 × 10⁻¹⁰ F
✅ Final Answer:
C = 1.0 × 10⁻¹⁰ F = 100 pF (approximately)
Types of Cylindrical Capacitors
Cylindrical capacitors are classified based on the type of dielectric material placed between their inner and outer cylinders. Each type has distinct characteristics, dielectric properties, and applications. Let’s explore the three major types below:
1️⃣ Air-Cored Cylindrical Capacitor
Dielectric Material: Air
Structure: Two hollow metallic cylinders separated by air.
Features:
- Simple and lightweight construction
- Very low dielectric constant (εᵣ ≈ 1)
- Offers low capacitance value
- Minimal dielectric losses
Applications:
- Used in RF circuits, oscillators, and testing setups
- Ideal where low capacitance and high frequency stability are required.
2️⃣ Solid Dielectric Cylindrical Capacitor
Dielectric Material: Solid materials such as mica, paper, ceramic, or plastic.
Structure: A compact cylindrical design with a solid insulating medium between the cylinders.
Features:
- Higher dielectric constant compared to air
- Provides greater capacitance for the same size
- Excellent stability, durability, and mechanical strength
Applications:
- Commonly used in power cables, electronic sensors, filter circuits, and high-voltage equipment.
3️⃣ Coaxial Cable Type Capacitor
Description: A coaxial cable behaves as a practical form of a cylindrical capacitor.
Structure:
- Inner conductor: Carries the main electrical signal.
- Outer conductor (shield): Serves as the return path or is grounded for safety.
- Dielectric: Insulating layer (commonly plastic or polyethylene) separates both conductors.
Applications:
- Extensively used in communication systems, signal transmission, and instrumentation cables.
- Ensures minimal signal loss and effective electromagnetic shielding.
🧠 Summary Table
| Type | Dielectric Material | Applications |
|---|---|---|
| Air-Cored | Air | RF circuits, oscillators, testing setups |
| Solid Dielectric | Mica, paper, ceramic, plastic | Power cables, sensors, filters |
| Coaxial Cable Type | Polyethylene or plastic | Communication and signal cables |
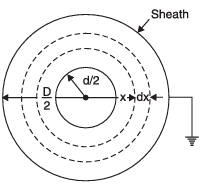
Potential Gradient in a Cylindrical Capacitor (Cable)
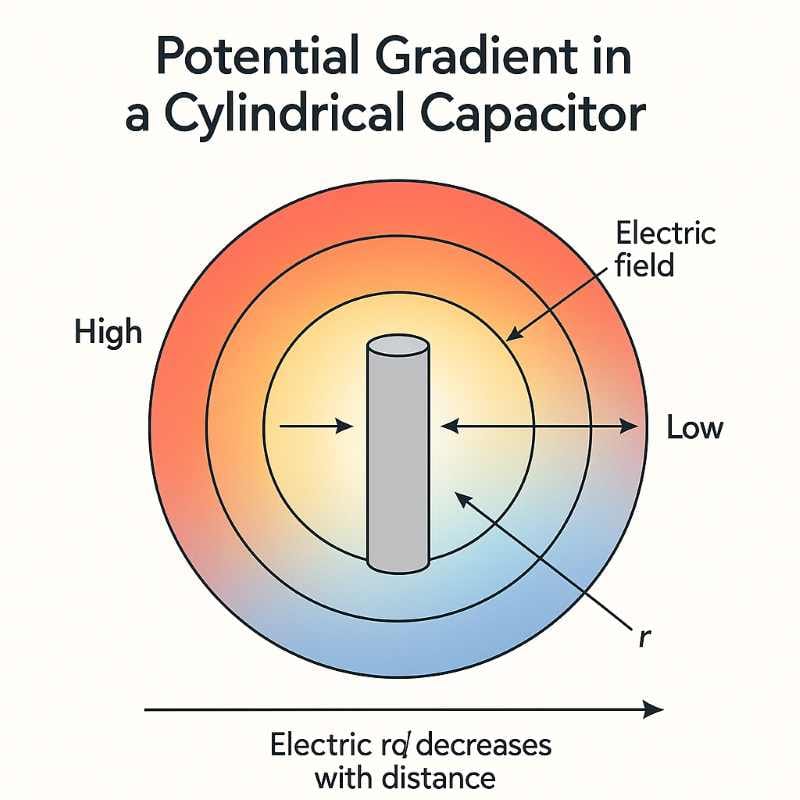
When electricity flows through a cable, the insulation around the conductor experiences an invisible electric force called dielectric stress. This stress represents the potential gradient—that is, how quickly the voltage changes from the center of the cable (the core) to its outer covering (the sheath).
You can imagine it like the slope of a slide — the steeper the slope, the faster you move. Similarly, the steeper the voltage change, the greater the dielectric stress at that point.
Understanding with a Cable Example
Consider a single-core cable:
- The inner wire (core) carries the electric current.
- Around it is an insulating layer that prevents leakage.
- Outside the insulation is a metal sheath that protects the cable and is often connected to the earth.
Let:
- Diameter of the core = d
- Inner diameter of the sheath = D
We want to understand how the potential gradient (electric stress) varies from the core to the sheath.
📉 Variation of Potential Gradient
The potential gradient is highest near the core and lowest near the sheath.
- At the surface of the core (x = d/2) → Maximum dielectric stress
- At the inner surface of the sheath (x = D/2) → Minimum dielectric stress
This happens because the voltage is distributed across the insulation. As we move outward, the same total voltage spreads over a larger radius, causing the gradient (or electric pressure) to decrease.
⚙️ Mathematical Insight
The electric field intensity (Eₓ) at a distance x from the center is given by:
Eₓ = Q / (2π ε₀ εᵣ x L)
This shows that Eₓ ∝ 1/x — meaning the electric field (or potential gradient) decreases as we move away from the core.
Hence:
- Maximum Potential Gradient (Emax): at x = a = d/2
- Minimum Potential Gradient (Emin): at x = b = D/2
Their ratio is:
Emax / Emin = b / a = D / d
Design Considerations in Cable Applications
When designing high-voltage cables:
- The maximum dielectric stress always occurs at the surface of the conductor.
- The insulation must be strong enough to withstand this maximum stress.
If the insulation strength is lower than the dielectric stress, it can lead to breakdown and cable failure.
For example: If the maximum potential gradient = 5 kV/mm, the insulation material must have a dielectric strength greater than 5 kV/mm to ensure safety and reliability.
Most Economical Conductor Size in a Cable
When designing an electrical cable, one of the most crucial components is the conductor — the central metallic wire that carries electric current. Selecting the correct conductor size is vital because it directly affects the dielectric stress (or electric pressure) on the surrounding insulation.
If this stress becomes too high, the insulation may fail, causing cable breakdown. To ensure reliability, the dielectric strength of the insulation must always be greater than the maximum electric stress acting on it.
🧩 Formula for Maximum Dielectric Stress
The maximum dielectric stress occurs at the surface of the conductor and is given by:
gₘₐₓ = (2V) / (d × ln(D/d))
Where:
- gₘₐₓ = Maximum dielectric stress (V/m)
- V = Operating voltage (volts)
- D = Inner diameter of the sheath (m)
- d = Diameter of the conductor (m)
- ln = Natural logarithm (base e)
⚙️ Finding the Most Economical Conductor Size
In most cable designs:
- The voltage (V) is fixed according to system requirements.
- The outer sheath diameter (D) is also fixed for insulation and safety reasons.
Therefore, the only adjustable parameter is the conductor diameter (d).
We aim to achieve minimum dielectric stress (gₘₐₓ) for safe and economical operation.
After mathematical analysis, gₘₐₓ is minimum when:
D/d = e (where e ≈ 2.718)
Hence, the most economical conductor diameter is:
d = D / 2.718
Under these conditions, the minimum maximum stress becomes:
gₘₐₓ(min) = (2V) / (2.718 × d)
This represents the lowest possible dielectric stress at the conductor surface — making it the most efficient and reliable cable design.
Design Considerations in Cable Applications
While the above gives a theoretical optimum, real-world cable design must also consider current-carrying capacity and thermal performance.
🔹 Low and Medium Voltage Cables
- The calculated optimum size may be too small for these cables.
- Smaller conductors carry less current and may overheat.
- Therefore, they’re determined mainly by current capacity and temperature limits, not just by dielectric stress or conductor size.
🔹 High Voltage Cables
- For HV systems, this formula gives a larger conductor size, which helps reduce stress and improve voltage distribution.
- Hence, it’s widely used for high-voltage cable design to ensure safety and long-term reliability.
How to Make Conductors More Economical
Since copper is costly, engineers use several strategies to reduce cost while maintaining efficiency:
1️⃣ Use Aluminium Instead of Copper
- Aluminium is cheaper and lighter than copper.
- For the same current, aluminium conductors are slightly thicker, helping reduce stress.
2️⃣ Use Stranded Copper Around a Core
- Instead of a solid copper rod, multiple fine copper strands are twisted around a non-metallic core (e.g., hemp or fiber).
- Reduces copper usage while maintaining strength and flexibility.
3️⃣ Use a Lead Tube in the Center
- A lead core provides mechanical strength and maintains the desired conductor diameter without using excessive copper.
🧠 Summary Table
| Parameter | Symbol | Typical Role |
|---|---|---|
| Conductor diameter | d | Determines maximum dielectric stress |
| Sheath inner diameter | D | Defines outer insulation boundary |
| Voltage | V | Determines electric stress level |
| Stress ratio | D/d | Most economical at 2.718 |
| Material | Cu / Al | Affects cost, weight, and performance |
Capacitance Between Parallel Wires
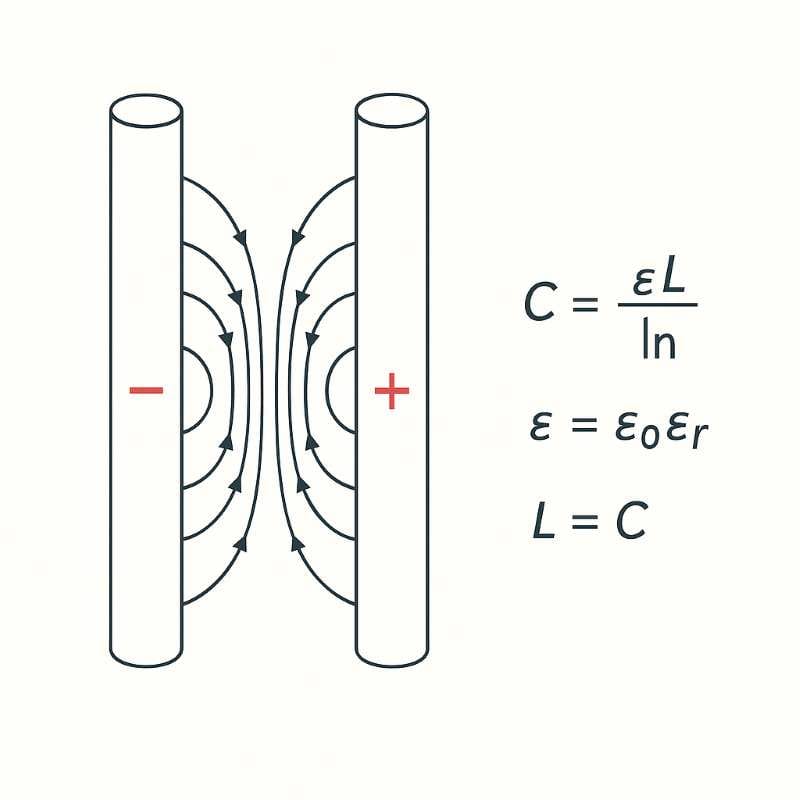
Imagine two long, straight wires running side by side in the air — like the power lines seen on poles or transmission towers. These wires are parallel, evenly spaced, and extend infinitely long.
Let’s call them Wire A and Wire B, each having a circular cross-section and carrying opposite charges:
- Wire A: positive charge (+Q)
- Wire B: negative charge (−Q)
Although the wires do not touch, they influence each other through the surrounding air, creating an electric field. This interaction results in capacitance — the ability to store electric charge between the wires.
💡 What is Capacitance?
Capacitance is the ability of two conductors to store electric charge per unit voltage between them.
For two parallel wires, capacitance depends on:
- Distance (d) between the wires → greater distance means lower capacitance.
- Radius (r) → Thicker wires can store more charge.
- Dielectric medium between the wires → materials with higher permittivity (ε) increase capacitance.
Think of capacitance as the tension in a stretched rubber band — the greater the separation, the more “tension” (voltage) needed to hold the same charge.
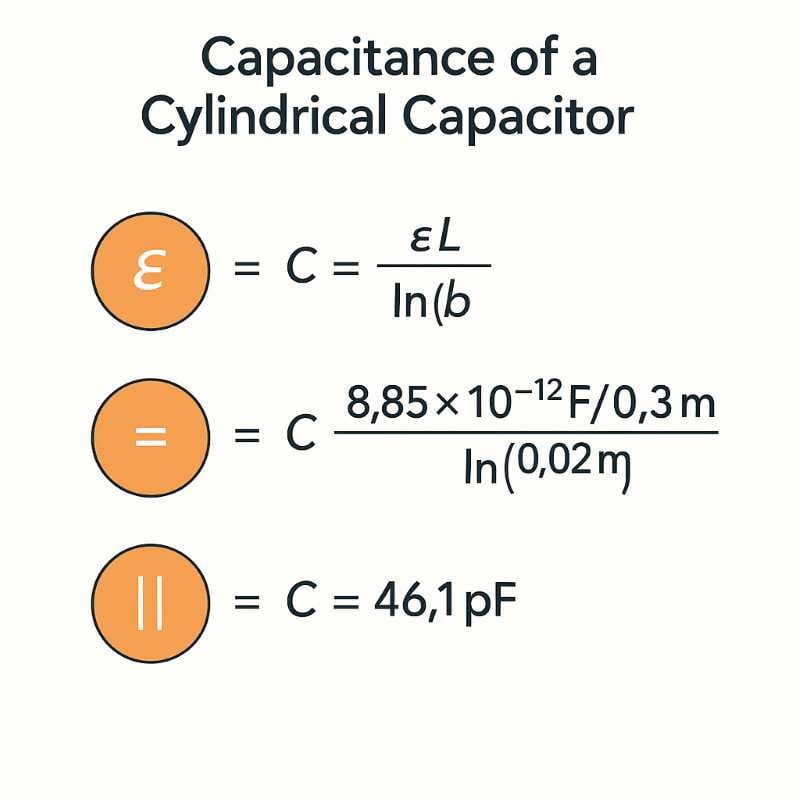
⚙️ Formula for Capacitance Between Two Parallel Wires
For two long parallel wires in air:
C = (π ε₀) / ln(d / r)
Unit: F/m
Where:
- C = Capacitance per meter length (F/m)
- ε₀ = Permittivity of free space = 8.854 × 10⁻¹² F/m
- d = Distance between wire centers (m)
- r = Radius of each wire (m)
📏 Observations
- As distance (d) increases → capacitance decreases.
- As wire radius (r) increases → capacitance increases.
- As permittivity (ε) of the medium increases → capacitance increases.
Thus, the capacitance between two wires depends primarily on spacing, size, and material properties of the medium.
Comparison Between Cylindrical Capacitor and Parallel Plate Capacitor
Capacitors come in various shapes and constructions based on their applications and design requirements. Two of the most common types are the Cylindrical Capacitor and the Parallel Plate Capacitor. The table below highlights their key differences in structure, function, and applications.
| Property | Cylindrical Capacitor | Parallel Plate Capacitor |
|---|---|---|
| Shape | Made of two concentric cylindrical conductors, one placed inside the other. | Made of two flat, parallel metallic plates separated by a dielectric. |
| Electric Field Pattern | Produces a radial electric field directed outward from the inner to the outer cylinder. | Has a uniform electric field between the plates. |
| Charge Distribution | Charge is distributed over curved surfaces of the cylinders. | Charge is distributed evenly on flat plates. |
| Formula for Capacitance | C = (2π ε₀ εᵣ L) / ln(b/a) | C = (ε₀ εᵣ A) / d |
| Dependent Parameters | Depends on length (L) and the ratio of radii (b/a). | Depends on plate area (A) and distance (d) between plates. |
| Electric Field Nature | Non-uniform, decreases with distance from the center. | Uniform throughout the dielectric region. |
| Dielectric Material | Air, oil, or plastic used between cylinders. | Air, mica, ceramic, or paper used between plates. |
| Applications | Used in cables, coaxial lines, and power transmission systems. | Used in electronic circuits, filters, sensors, and energy storage devices. |
| Practical Example | Found in single-core or coaxial cables. | Found in basic circuit board capacitors. |
🧩 Insulation Resistance of a Cable Capacitor
Inside a cable, a metallic conductor carries current and is surrounded by insulation that prevents current leakage.
🧠 Why is Insulation Important?
The insulation acts as a protective barrier, preventing current from leaking into the surrounding medium — similar to how a waterproof jacket keeps you dry.
The effectiveness of this insulation is measured by its insulation resistance (R).
⚙️ Formula for Insulation Resistance
For a single-core cable:
R = (ρ / (2πl)) × ln(r₂ / r₁)
Unit: Ω
Where:
- R = Insulation resistance (Ω)
- ρ = Resistivity of insulating material (Ω·m)
- l = Length of cable (m)
- r₁ = Radius of conductor (m)
- r₂ = Inner radius of sheath (m)
📉 Effect of Cable Length
- Longer cable → lower insulation resistance
- Shorter cable → higher insulation resistance
Hence, long cables must always be tested for insulation quality to ensure safety.
| Condition | Effect on Insulation Resistance (R) |
|---|---|
| Long cable | Lower insulation resistance |
| Short cable | Higher insulation resistance |
| High resistivity material | Better insulation |
✅ Good insulation = High resistance = Safe cable
❌ Poor insulation = Low resistance = Leakage risk
Limitations of the Cylindrical Capacitor
While cylindrical capacitors are extremely useful in power systems, high-voltage cables, and transmission designs, they also have several limitations that affect their theoretical analysis and real-world applications.
1️⃣ Dependence on Geometry
The capacitance of a cylindrical capacitor is highly dependent on its physical dimensions — particularly the radii of the cylinders and their length (L).
- Small changes in dimensions can significantly affect the capacitance value.
- This makes it difficult to miniaturize or precisely control capacitance in compact or microelectronic circuits.
Impact: Cylindrical capacitors are less suitable for precision electronic applications that require consistent and tunable capacitance.
2️⃣ Edge Effects Ignored
The standard theoretical formula for capacitance assumes that the capacitor is infinitely long, which means edge effects are neglected.
- In real-world scenarios, the ends of the cylinders cause electric field distortions, altering charge distribution.
- These edge effects lead to slight errors in capacitance calculation and performance estimation.
Impact: The formula C = (2π ε₀ εᵣ L) / ln(b/a) is only accurate for long cylinders; short cables or finite-length designs require correction factors.
3️⃣ Non-Uniform Electric Field
The electric field inside a cylindrical capacitor is radial and non-uniform — it is strongest near the inner conductor and weakest near the outer sheath.
- This non-uniform field distribution makes analytical modeling and simulation more complex.
- In contrast, parallel-plate capacitors have uniform fields, simplifying calculations and designs.
Impact: The non-uniform field introduces computational challenges in theoretical and numerical analysis, particularly in high-frequency and transient studies.
✅ Summary Table
| Limitation | Explanation |
|---|---|
| Dependence on geometry | Difficult to miniaturize or precisely control capacitance due to reliance on cylinder size and spacing. |
| Edge effects ignored | The formula is valid only for long cylinders; real cables have end effects that slightly alter capacitance. |
| Non-uniform field | The formula valid only for long cylinders; real cables have end effects that slightly alter capacitance. |
🏭 Applications of Cylindrical Capacitors
Cylindrical capacitors are not just theoretical — they are used in various electrical and electronic systems.
🔋 Power Electronics
- Used for energy storage, filtering, and voltage regulation in power converters, UPS systems, and motor drives.
⚙️ Motors and HVAC Systems
- Provide phase shift for starting and running single-phase motors.
- Found in air conditioners, fans, and refrigerators.
💡 Lighting Systems
- Used in LED drivers and fluorescent lamps for power factor correction and signal filtering.
🎧 Audio Equipment
- Maintain clear sound output in amplifiers and crossovers by filtering unwanted frequencies.
🏭 Industrial Equipment
- Used in capacitor banks for power factor correction and voltage stabilization in heavy machinery.
💻 Electronics
- Commonly used in computers, TVs, and radios for timing, decoupling, and noise suppression.
🏥 Medical Devices
- Used in defibrillators and imaging systems to safely deliver quick, high-energy pulses.
✅ Why Cylindrical Shape?
- Ensures uniform electric field distribution between electrodes.
- Provides better heat dissipation and a compact design.
- Easy to mount vertically or horizontally in electronic circuits.
FAQ
I am an Electrical Engineer with qualifications in ITI, Diploma, and B.Tech. I have worked as an ITI college instructor for 3 years and have over 5 years of hands-on experience in the electrical field. The information shared on this website is based on trusted electrical engineering textbooks such as P.S. Bimbhra, B.L. Theraja, V.K. Mehta, and real-world practical experience.