Table of Contents
Measurement of Power in Three-Phase Systems
A wattmeter is a device used to measure the average or real power in AC circuits. While the method for measuring single-phase power is discussed in Chapter 1, this section focuses on the measurement of three-phase power.
There are three main methods used for measuring the active (real) power in a three-phase system:
- Three Wattmeter Method
- Two Wattmeter Method
- One Wattmeter Method
✅ Three wattmeter Method and two wattmeter methods can be used for both balanced and unbalanced systems.
✅ The one wattmeter method is applicable only for balanced systems.
Each method has its own applications depending on the type of load and system balance.
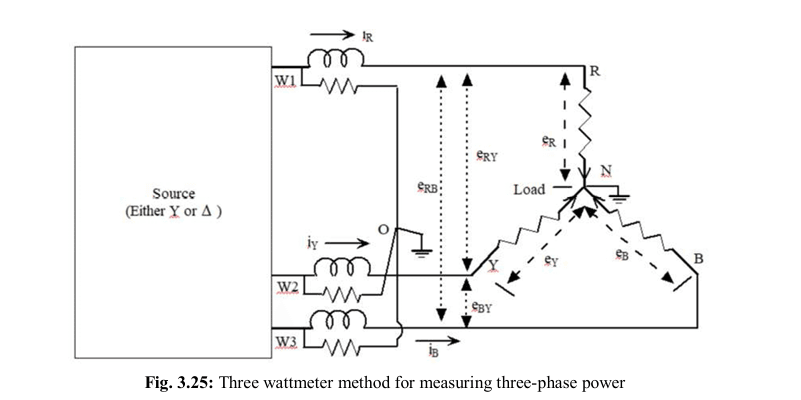
Three Wattmeter Method
In Measurement of Power in Three-Phase Systems, three wattmeters are used. These wattmeters are connected as shown in Fig. 3.25. Although the figure shows a star-connected load, this method is also applicable to a delta (Δ) connected load.
In a balanced load condition, the real power in each phase is the same. So, in such cases, you could technically measure power using just one wattmeter on any one of the phases. However, when all three wattmeters are used:
- Let:
- P₁, P₂, and P₃ be the power in phase R, Y, and B, respectively.The total three-phase real power, denoted as P₃ϕ, is:
In the three wattmeter method, the power measured by each wattmeter is denoted as W₁, W₂, and W₃. These correspond to each phase.
So, the total real power for a balanced three-phase load is:
P3ϕ=W1+W2+W3
This equation shows that the sum of readings of all three wattmeters gives the total three-phase real power.
If the load is balanced, the real power can also be calculated using the formula:
P=3⋅VL⋅IL⋅cosϕ =
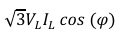
Where:
- VL = Line Voltage
- IL = Line Current
- cosϕ = Power factor of the load
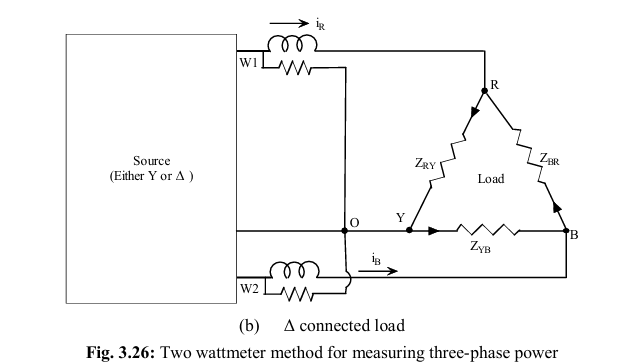
Two Wattmeter Method (for Measuring Power in 3-Phase Systems)
The Two Wattmeter Method is a popular technique used to measure the total power in a three-phase, three-wire system—whether the load is balanced or unbalanced.
How It Works:
- Two wattmeters are used.
- The current coil of each wattmeter is connected in two of the three-phase lines (say R and B).
- The potential coil (voltage coil) of each wattmeter is connected between:
- Wattmeter 1: Between R and Y
- Wattmeter 2: Between B and Y
This connection setup allows each wattmeter to measure a portion of the total power. The sum of the two wattmeter readings gives the total power of the three-phase system.
Diagram Reference:
Imagine a three-phase supply with R, Y, and B lines:
Wattmeter W1:
Current coil → R-line
Potential coil → between R and Y
Wattmeter W2:
Current coil → B-line
Potential coil → between B and YTotal Power:
The total power (P) in the 3-phase system is the algebraic sum of the readings of the two wattmeters:
P = W1 + W2This method works for both balanced and unbalanced loads and is especially popular in practical power measurements due to its simplicity and accuracy.
Connection Summary:
| Wattmeter | Current Coil Connection | Potential Coil Connection |
|---|---|---|
| W1 | Line R | Between R and Y |
| W2 | Line B | Between B and Y |
Important Notes:
- The method works for both balanced and unbalanced loads.
- The total power in the system is:
P total=W1+W2 - If the load is balanced and power factor is known, you can also calculate the power factor using the wattmeter readings.
Two-Wattmeter Method – Basic Setup
Configuration:
- Wattmeter W1:
- Current coil in line R
- Potential coil between R and Y
- Wattmeter W2:
- Current coil in line B
- Potential coil between B and Y
This setup is typically used to measure total power in a 3-phase system.
🧮 Instantaneous Values
Let:
- iR, iY, and iB be line currents in R, Y, and B respectively.
- vRY, vBY are line voltages between R-Y and B-Y.
Then:
Wattmeter W1:
- Instantaneous current: iR
- Instantaneous voltage: vRY=vR−vY
- Instantaneous power:
- W1=iR(vR−vY)
Wattmeter W2:
- Instantaneous current: iB
- Instantaneous voltage: vBY=vB−vY
- Instantaneous power:
- W2=iB(vB−vY)
🔄 Total Instantaneous Power
W1+W2=iR(vR−vY)+iB(vB−vY)
Expand:=iRvR−iRvY+iBvB−iBvY
(iRvR+iBvB)−vY(iR+iB)
Now, apply Kirchhoff’s Current Law for a balanced 3-phas
system: iR+iY+iB=0⇒iR+iB=−iY
So: W1+W2=iRvR+iBvB+iYvY
Thus:W1+W2=Total instantaneous 3-phase power
This result is true for both balanced and unbalanced loads, and for Y or Δ-connected loads (since Δ can be converted to equivalent Y).
✅ Special Case: Balanced Load
Let the phase voltages and currents be:
- VR=Vm∠0∘
- VY=Vm∠−120∘
- VB=Vm∠+120∘
Assume impedance Z=∣Z∣∠θ, so current lags by θ
- IR=Im∠−θ
- IY=Im∠−120∘−θ
- IB=Im∠+120∘−θ
Then:W1=VLILcos(30∘−θ)
W2=VLILcos(30∘+θ)
Where:
- VL: Line voltage
- IL: Line current
Total Power: W1+W2=VLIL[cos(30∘−θ)+cos(30∘+θ)]= 2VLILcos30∘cosθ
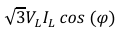
3Vph,Iph,cosθ
Which is the standard 3-phase power formula.
- Two-wattmeter method is a versatile technique for measuring 3-phase power.
- Works for balanced or unbalanced, star or delta loads.
- Wattmeters measure power using line current and line-to-line voltage.
- The sum of both wattmeter readings gives total 3-phase power.
Let me know if you’d like a diagram, animation prompt, or Hindi version for educational use.
Phasor Diagram (Star Connection – Two Wattmeter Method)
In a balanced three-phase star-connected load, the line voltages lead their respective phase voltages by 30°. The current is in phase with the phase voltage (for purely resistive loads), or it leads/lags depending on the power factor.
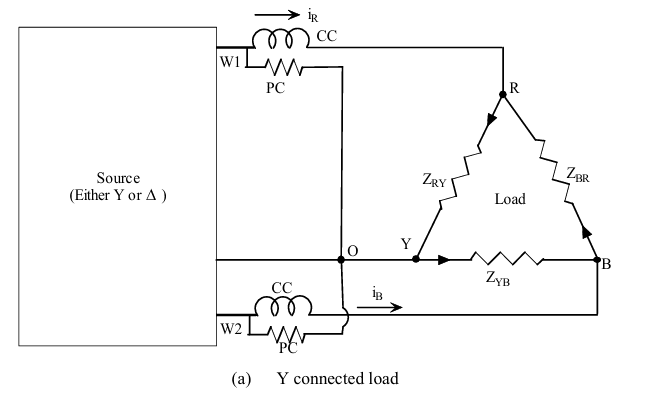
Phasors in the Diagram:
- Phase voltages (Vph): Va, Vb, Vc
- Line voltages (VL): Vab, Vbc, Vca
- Line currents (IL): Ia, Ib, Ic
The two wattmeters are connected as:
- W1 measures power in line A (with voltage Vab and current Ia)
- W2 measures power in line C (with voltage Vcb and current Ic)
📐 Mathematical Formulas
Power measured by Wattmeter-1 (W1):
P1=VL⋅IL⋅cos(ϕ+30∘)
Power measured by Wattmeter-2 (W2):
P2=VL⋅IL⋅cos(ϕ−30∘)
Total Real Power (P):
P=P1+P2=3⋅VL⋅IL⋅cos(ϕ)
This is the total three-phase real (active) power.
Reactive Power (Q₃Φ):
Using the difference between the wattmeter readings:
P1−P2=VL⋅IL[cos(ϕ+30∘)−cos(ϕ−30∘)]=−2VL⋅IL⋅sin(ϕ)⋅sin(30∘)
Simplifies to:
P1−P2=VL⋅IL⋅sin(ϕ)
Q3ϕ=^3(P1−P2)
Apparent Power (S):
S=^(P2+Q2)
Power Factor Angle (φ):
tan(ϕ)=3^(P1−P2)/P1+P2
Power Factor (cos φ):

⚡ Load Type Based on Wattmeter Readings
| Condition | Nature of Load | Explanation |
|---|---|---|
| P1=P2 | Resistive | Power factor is unity |
| P1>P2 | Inductive | Lagging power factor (positive φ) |
| P1<P2 | Capacitive | Leading power factor (negative φ) |
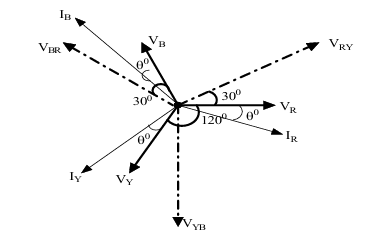
Sure! Here’s a clearer and more organized explanation of the One Wattmeter Method for measuring three-phase power, based on the text you provided:
One Wattmeter Method for Balanced Load Systems
The one wattmeter method is applied only for balanced three-phase load systems.
Connection Setup:
- The current coil of the wattmeter is connected to one of the phase lines — for example, the R phase.
- The potential coil is connected between the R phase and a node (Node 1).
- Node 1 can be connected either to Node 2 or Node 3, resulting in two different voltage measurements.
When:
- Node 1 is connected to Node 2, the wattmeter reading is denoted as W1.
- Node 1 is connected to Node 3, the wattmeter reading is denoted as W2.
Thus, two wattmeter readings are obtained: W1 and W2.
Measurement and Power Calculation
- These two wattmeter readings correspond to the active power components in the system.
- The sum of the two wattmeter readings gives the total three-phase active power (P).
Mathematically: W1+W2=P1+P2
Where:
- P1 = Power measured when Node 1 is connected to Node 2.
- P2= Power measured when Node 1 is connected to Node 3.
The phasor relationships and voltages can be derived from the balanced system conditions and the two-wattmeter method equations, leading to:
W1+W2=3VphIphcosϕ=3Pph
Here,
- Vph = Phase voltage
- Iph = Phase current
- ϕ = Phase angle between current and voltage
- Pph = Active power per phase
Because the load is balanced:
IR+IY+IB=0
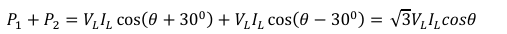
Summary:
- The one wattmeter method uses two different connections of the potential coil to measure two power values, W1 and W2
- The sum W1+W2 gives the total active power in a balanced three-phase system.
- This method relies on the balanced load condition and the two-wattmeter method principles.
If you want, I can also help with drawing or explaining the connection diagrams or the phasor diagrams referenced! Would that help?
TYPES OF CONNECTIONS IN THREE-PHASE SYSTEMS
The three-phase power supply is generated from the three coils, which are mentioned at the beginning of this chapter. The generated power is utilized by the three-phase loads. The different connections could be achieved between the three-phase source and load as follows.
star (Y) – star (Y)
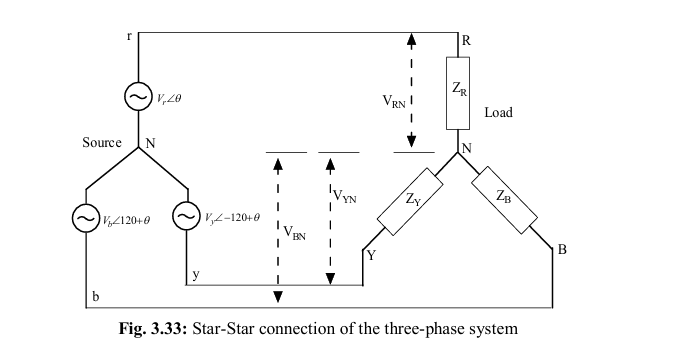
star (Y) – delta(Δ)
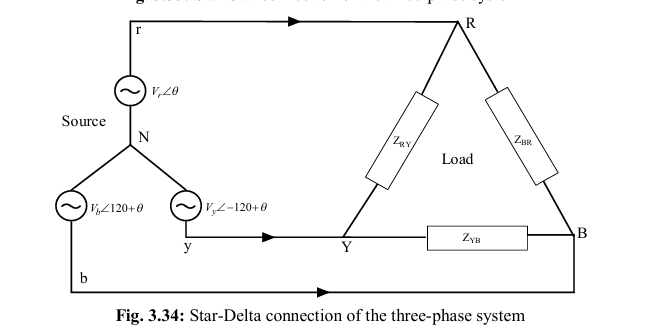
delta (Δ)- star (Y)
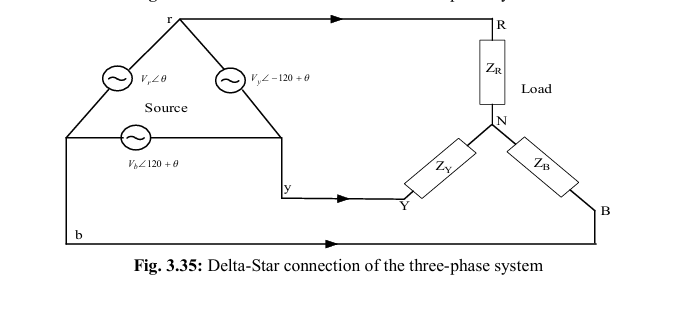
delta (Δ)- delta (Δ)

Key Concepts in Three-Phase Systems
- Phase Sequence
The phase sequence refers to the order in which the voltages in a three-phase system reach their maximum (peak) values with respect to time.
There are two types of phase sequences:
Positive Phase Sequence: Standard sequence (e.g., R → Y → B).
Negative Phase Sequence: Occurs when any two phases are interchanged.
2. Line and Phase Quantities
Line Current (IL): The current flowing in each transmission line from the generator to the load.
Line Voltage (VL): The voltage between any two lines, not including the neutral line (if present).
Phase Current (Iph): The current in each phase winding or load.
Phase Voltage (Vph): The voltage across each phase element in the load.
3. Three-Phase Connections
Three-phase systems can be connected in:
Star (Y) connection
Delta (Δ) connection
In a balanced system, the total instantaneous power remains constant and equals the average power.
4. Power Measurement in Three-Phase Systems
Real power in a three-phase system can be measured using:
The Three-Wattmeter Method (for any load)
The Two-Wattmeter Method (commonly used for balanced or unbalanced loads)
In a balanced load, the total real power equals the sum of the two wattmeter readings in the two-wattmeter method.
5. Unbalanced System Analysis
Unbalanced three-phase systems require more advanced analysis techniques such as:
Nodal Analysis
Mesh Analysis
FAQ
I am an Electrical Engineer with qualifications in ITI, Diploma, and B.Tech. I have worked as an ITI college instructor for 3 years and have over 5 years of hands-on experience in the electrical field. The information shared on this website is based on trusted electrical engineering textbooks such as P.S. Bimbhra, B.L. Theraja, V.K. Mehta, and real-world practical experience.