Table of Contents
INTRODUCTION
When we look at the many different things we measure in science—like speed, temperature, or weight—it may seem like we need a different unit for each one. But if we try to make a unique unit for every single thing, remembering all those units would become very confusing and nearly impossible.
Luckily, many of these physical quantities are connected to each other. For example, speed is not something completely separate—it depends on distance and time. In simple words, speed is how much distance something covers in a certain time (Speed = Distance ÷ Time). So, instead of creating a new unit for speed, we can just use the units of distance and time.
This idea helps us a lot. In fact, most of the measurements in mechanics (the science of motion and forces) can be expressed using just three basic things: length, mass, and time. These three are completely different from one another. You cannot turn mass into time or time into length. Each one stands on its own. That’s why we call them fundamental quantities, and the units we use to measure them are called fundamental units.
Now, when we move to other areas of science—like electricity, heat, and light—we need to add a few more fundamental quantities. These are:
- Electric current
- Temperature
- Luminous intensity (which means how bright a light is)
These are also independent and have their own special units. Just like the earlier three, they are also called fundamental quantities, and their units are fundamental units.
Later, in 1971, scientists agreed that one more thing should be added to this list: the amount of substance (which is used when we count very tiny particles like atoms or molecules). A basic unit was also decided for this quantity.
What is SI Unit system List?
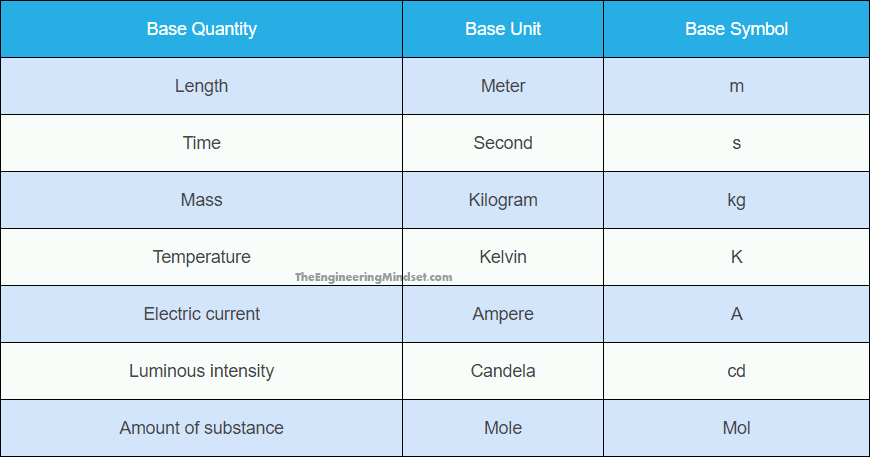
So, in total, there are seven fundamental quantities in the SI (International System of Units). Each of these has its own unique and basic unit:
- Length – meter (m)
- Mass – kilogram (kg)
- Time – second (s)
- Electric current – ampere (A)
- Temperature – kelvin (K)
- Luminous intensity – candela (cd)
- Amount of substance – mole (mol)
All other units we use in science are made by combining these seven. That’s why these seven are called the building blocks of measurement.
Meter (m): A Unit of Length
The meter is the basic unit used to measure length or distance. You can think of it as how far you might walk in a big step. It helps us know how long, tall, or wide something is.
How is 1 Meter Defined?
Long ago, scientists decided to define a meter in a very special way.
They said:
1 meter is the length of 1,650,763.73 waves of orange light given off by a gas called krypton-86.
That’s just a fancy way of saying it’s super accurate — and used the same everywhere in the world!
Bigger and Smaller Units of Length
Sometimes, 1 meter is too big or too small for what we want to measure. That’s why we have different units. Let’s take a look:
Bigger Units:
- 1 kilometer (km) = 1,000 meters
(Used to measure long distances like roads or cities.)
🔸 Smaller Units:
- 1 decimeter (dm) = 0.1 meter
(About the length of a pencil stub.) - 1 centimeter (cm) = 0.01 meter
(Used to measure things like your fingers or books.) - 1 millimeter (mm) = 0.001 meter
(Used for tiny things like the thickness of a coin.) - 1 micron (μm) = 0.000001 meter
(Used for cells or dust particles.) - 1 nanometer (nm) = 0.000000001 meter
(Used to measure atoms and tiny wavelengths of light.) - 1 angstrom (Å) = 0.0000000001 meter
(Used in physics and chemistry for very, very tiny distances.)
What is a Light Year?
A light year is not about time — it’s about distance!
It means: How far light travels in one year.
Light moves super fast: about 300,000,000 meters per second.
So in one year, light can travel a huge distance.
✨ 1 Light Year =
300,000,000 meters/second × 365 days × 24 hours × 60 minutes × 60 seconds
= 9.46 trillion kilometers
= 9.46 × 10¹⁵ meters
That’s how big the universe is — we need “light years” to measure it!
✅ Quick Summary
| Unit | Equals in Meters | Use Case |
|---|---|---|
| 1 kilometer (km) | 1,000 m | Long distances (cities, roads) |
| 1 meter (m) | 1 m | Standard unit |
| 1 decimeter (dm) | 0.1 m | Small lengths |
| 1 centimeter (cm) | 0.01 m | Books, small objects |
| 1 millimeter (mm) | 0.001 m | Tiny things like seeds |
| 1 micron (μm) | 0.000001 m | Micro-level particles |
| 1 nanometer (nm) | 0.000000001 m | Molecules, light waves |
| 1 angstrom (Å) | 0.0000000001 m | Atoms and tiny structures |
| 1 light year | 9.46 × 10¹⁵ m | Distances in space |
The Kilogram – Unit of Mass
The kilogram is the standard unit of mass. Historically, it was defined as the mass of a specific platinum-iridium cylinder kept in Paris.
In practice, 1 kilogram is approximately the mass of 1 litre (1000 cm³) of water at 4°C.
On the atomic scale, 1 kilogram is equal to the mass of approximately 5.0188 × 10²⁵ atoms of carbon-12 (C-12).
To make measurements more convenient, several larger and smaller units of mass have been derived from the kilogram:
- 1 metric ton = 1000 kilograms (kg)
- 1 quintal = 100 kilograms (kg)
- 1 gram (g) = 1⁄1000 of a kilogram (0.001 kg)
- 1 milligram (mg) = 1⁄1000 of a gram (0.000001 kg)
Second (s):
It is a unit of time. One second is defined as the duration in which a cesium-133 atom makes 9,192,631,770 vibrations (or transitions between two energy levels).
There are several larger and smaller units of time as well:
- 1 hour = 3600 seconds
- 1 minute = 60 seconds
- 1 millisecond (ms) = 10⁻³ seconds
- 1 microsecond (µs) = 10⁻⁶ seconds
- 1 nanosecond (ns) = 10⁻⁹ seconds
- 1 picosecond (ps) = 10⁻¹² seconds
The system of units based on the three fundamental mechanical quantities—meter (m), kilogram (kg), and second (s)—is called the MKS system (Meter-Kilogram-Second system of units).
Ampere (A):
It is the unit of electric current. One ampere is defined as the current that, when flowing through two parallel wires of infinite length placed 1 meter apart in a vacuum, produces a force of 2×10−72 newtons per meter of length between the wires.
The system of units based on these four fundamental units is called the Metre-Kilo-Second-Ampere (MKSA) system.
Kelvin (K):
Kelvin is the unit of temperature. One kelvin is defined as 1/273.161 of the thermodynamic temperature of the triple point of water.

Candela (cd):
Candela is the unit of luminous intensity. One candela is defined as the luminous intensity of a surface area of a black body (a standard light source) measuring 1/600,000 meter in a direction perpendicular to the surface, when the black body’s temperature is at the melting point of platinum.
Mole:
A mole is the unit used to measure the quantity of a substance. One mole contains exactly the same number of entities (such as atoms, molecules, or ions) as there are atoms in 0.012 kilograms of carbon-12 (12C).
Complementary Units:
In addition to the fundamental units mentioned above, there are two complementary units related to angles:
Radian:
One radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius of the circle.
Steradian (sr):
One steradian is the solid angle at the center of a sphere that subtends an area on the surface of the sphere equal to the square of the radius of the sphere.
Derived Units
We know some basic things we can measure, like length, mass, time, electric current, temperature, light brightness, and amount of stuff. These are called fundamental units because they are the basic building blocks.
But what about other things we want to measure, like how fast something is moving, how heavy something feels compared to its size, or how much work is done? For these, we use derived units. Derived units are made by combining the basic units in different ways.
Here are some examples of derived units:

Volume
Volume tells us how much space something takes up.
To find volume, we multiply length × width × height.
So, the unit of volume is metre × metre × metre, which is called a cubic metre (m³).
Density
Density tells us how heavy something is compared to its size.
It is found by dividing mass by volume.
So, the unit of density is kilogram per cubic metre (kg/m³).
Velocity
Velocity means how fast something is moving and in which direction.
It is displacement (distance moved) divided by time taken.
The unit of velocity is metre per second (m/s).
Acceleration
Acceleration tells us how quickly the speed of something changes.
It is velocity change divided by time taken.
The unit of acceleration is metre per second squared (m/s²).
Force
Force means a push or pull on an object.
It is found by multiplying mass by acceleration.
The unit of force is kilogram metre per second squared (kg·m/s²), which is also called a newton (N).

Work
Work means how much force is used to move something.
It is force multiplied by displacement (distance moved).
The unit of work is newton metre (N·m), which is called a joule (J).
Energy also uses the same unit as work.
Power or potential work/time
Power is how fast work is done or energy is used over time. Think of it like how quickly you can finish a task. If you do a lot of work in a short time, your power is high. If it takes a long time to do a little work, your power is low.
How do we measure power?
The unit we use to measure power is called a watt. One watt means one joule of work done in one second.
So, if you do 1 joule of work in 1 second, you are using power at a rate of 1 watt.
In short:
Power = Work ÷ Time
And the unit is:
1 watt = 1 joule / 1 second
Dimensions of Physical Quantities
When we talk about physical things like speed or length, we use units to measure them. For example, speed can be written as kilometers per hour or meters per second. But no matter how we write it, speed always means how much distance is covered in a certain amount of time.
To show this clearly, we say:
Unit of speed = Unit of length ÷ Unit of time
For example, if you run 5 kilometers in 1 hour, your speed is 5 kilometers per hour.
Now, when we talk about the dimensions of speed, we mean the powers or how many times the units of length and time are used.
For speed:
- The length is used once (power of 1)
- The time is used once, but in the denominator (also power of 1, but because it’s in the bottom, it’s like divided)
So, the dimensions of speed are written as:
Length¹ × Time⁻¹
This means speed depends on length and time — length goes up, and time goes down.
Dimensions of SI Unit system
Whatever units of length and time are chosen, the dimensions of any physical quantity are the powers to which the basic units must be raised to express the unit of that quantity.
To write the dimensions of physical quantities used in mechanics and thermodynamics, the fundamental units are represented as follows:
- Length → L
- Mass → M
- Time → T
- Temperature → θ
If the dimensions of a physical quantity are a in length, b in mass, t in time, and v in temperature, then the dimensional formula of that quantity is written as:
[Lᵃ Mᵇ Tᵗ θᵛ]
This expression is called the dimensional formula of the physical quantity.
Dimensional Formula of Physical Quantities
To find the dimensional formula of any physical quantity, we express that quantity in terms of other simple physical quantities whose dimensions are already known. Below are the dimensional formulas of some commonly used physical quantities:
(You can follow this with a table or list of examples, such as Force, Work, Energy, Power, etc.)
1. Area
Formula: Length × Width
Meaning: The amount of space a surface covers.
Unit: Square meter (m²)
Dimensional Formula: [L²]
2. Volume
Formula: Length × Width × Height (or Thickness)
Meaning: The amount of space an object takes up.
Unit: Cubic meter (m³)
Dimensional Formula: [L³]
3. Velocity (or Speed with Direction)
Formula: Distance / Time
Meaning: How fast something is moving in a specific direction.
Unit: Meter per second (m/s)
Dimensional Formula: [LT⁻¹]
4. Acceleration
Formula: Change in Velocity / Time
Meaning: How quickly speed increases or decreases.
Unit: Meter per second squared (m/s²)
Dimensional Formula: [LT⁻²]
5. Force
Formula: Mass × Acceleration
Meaning: A push or pull acting on a body.
Unit: Newton (N)
Dimensional Formula: [MLT⁻²]
6. Work
Formula: Force × Displacement
Meaning: When force moves an object, work is done.
Unit: Joule (J)
Dimensional Formula: [ML²T⁻²]
7. Power
Formula: Work / Time
Meaning: How fast work is done.
Unit: Watt (W)
Dimensional Formula: [ML²T⁻³]
8. Density
Formula: Mass / Volume
Meaning: How much mass is packed in a given space.
Unit: Kilogram per cubic meter (kg/m³)
Dimensional Formula: [ML⁻³]
9. Momentum
Formula: Mass × Velocity
Meaning: The quantity of motion an object has.
Unit: kg·m/s
Dimensional Formula: [MLT⁻¹]
10. Kinetic Energy
Formula: ½ × Mass × Velocity²
Meaning: Energy due to motion.
Unit: Joule (J)
Dimensional Formula: [ML²T⁻²]
11. Gravitational Potential Energy
Formula: Mass × Gravity × Height
Meaning: Energy stored due to position above ground.
Unit: Joule (J)
Dimensional Formula: [ML²T⁻²]
12. Pressure
Formula: Force / Area
Meaning: Force applied on a surface per unit area.
Unit: Pascal (Pa)
Dimensional Formula: [ML⁻¹T⁻²]
13. Impulse
Formula: Force × Time
Meaning: The effect of force acting over time.
Unit: Newton-second (N·s)
Dimensional Formula: [MLT⁻¹]
14. Torque
Formula: Force × Distance (from axis of rotation)
Meaning: A force that causes rotation.
Unit: Newton-meter (N·m)
Dimensional Formula: [ML²T⁻²]
15. Stress
Formula: Force / Area
Meaning: Force per unit area within a body.
Unit: Pascal (Pa)
Dimensional Formula: [ML⁻¹T⁻²]
16. Strain
Formula: Change in Length / Original Length
Meaning: How much an object stretches or compresses.
Unit: No unit (it’s a ratio)
Dimensional Formula: Dimensionless (No dimensions)
17. Modulus of Elasticity
Formula: Stress / Strain
Meaning: It tells us how stiff a material is — how much it resists being stretched or squeezed.
Unit: Pascal (Pa)
Dimensional Formula: [M L⁻¹ T⁻²]
18. Surface Tension
Formula: Force / Length
Meaning: It measures how strong the surface of a liquid is, like a thin skin that holds it together.
Unit: Newton per meter (N/m)
Dimensional Formula: [M T⁻²]
19. Gravitational Constant (G)
Formula: Force × Distance² / (Mass × Mass)
Meaning: It shows how strong the pull of gravity is between two objects.
Unit: Newton meter² per kilogram² (N·m²/kg²)
Dimensional Formula: [M⁻¹ L³ T⁻²]
20. Gravitational Field Strength
Formula: Force / Mass
Meaning: It tells the strength of gravity at a point, like how hard gravity pulls on one kilogram of mass.
Unit: Meter per second squared (m/s²)
Dimensional Formula: [L T⁻²]
21. Gravitational Potential
Formula: Potential Energy / Mass
Meaning: It is the energy per kilogram at a point due to gravity.
Unit: Joule per kilogram (J/kg)
Dimensional Formula: [L² T⁻²]
22. Force Constant of Spring (k)
Formula: Force / Extension
Meaning: It tells how stiff a spring is — how much force it needs to stretch by a certain length.
Unit: Newton per meter (N/m)
Dimensional Formula: [M T⁻²]
23. Frequency
Formula: 1 / Period
Meaning: It shows how many times something repeats in one second, like the number of waves or vibrations.
Unit: Hertz (Hz)
Dimensional Formula: [T⁻¹]
24. Angle in Radians
Formula: Arc length / Radius
Meaning: It tells the size of an angle based on how much of a circle’s edge it covers compared to the radius.
Unit: Radian (rad) — no unit
Dimensional Formula: Dimensionless
25. Angular Velocity
Formula: Angle / Time
Meaning: It tells how fast something is spinning or rotating.
Unit: Radian per second (rad/s)
Dimensional Formula: [T⁻¹]
26. Angular Acceleration
Formula: Change in Angular Velocity / Time
Meaning: It shows how quickly the spinning speed is changing.
Unit: Radian per second squared (rad/s²)
Dimensional Formula: [T⁻²]
27. Moment of Inertia
Formula: Mass × (Distance)²
Meaning: It tells how hard it is to spin an object around an axis.
Unit: Kilogram meter squared (kg·m²)
Dimensional Formula: [M L²]
28. Angular Momentum
Formula: Moment of Inertia × Angular Velocity
Meaning: It shows how much rotation an object has and how hard it is to stop it spinning.
Unit: Kilogram meter squared per second (kg·m²/s)
Dimensional Formula: [M L² T⁻¹]
29. Specific Heat
Formula: Thermal Energy / (Mass × Temperature Rise)
Meaning: It tells how much heat energy is needed to raise the temperature of one kilogram of a substance by one degree.
Unit: Joule per kilogram kelvin (J/kg·K)
Dimensional Formula: [L² T⁻² Θ⁻¹]
Derived Quantities in Physics list of SI Unit system
Each of these is made by combining simple quantities like length, mass, or time.
| S. No. | Derived Quantity | Formula or Relation | Dimensional Formula |
|---|---|---|---|
| 1. | Area | Length × Width | [L²] |
| 2. | Volume | Length × Width × Height (or Thickness) | [L³] |
| 3. | Velocity (Speed with direction) | Distance ÷ Time | [LT⁻¹] |
| 4. | Acceleration | Change in Velocity ÷ Time | [LT⁻²] |
| 5. | Force | Mass × Acceleration | [MLT⁻²] |
| 6. | Work | Force × Distance | [ML²T⁻²] |
| 7. | Power | Work ÷ Time | [ML²T⁻³] |
| 8. | Density | Mass ÷ Volume | [ML⁻³] |
| 9. | Momentum | Mass × Velocity | [MLT⁻¹] |
| 10. | Kinetic Energy | ½ × Mass × Velocity² | [ML²T⁻²] |
| 11. | Gravitational Potential Energy | Mass × Gravity × Height | [ML²T⁻²] |
| 12. | Pressure | Force ÷ Area | [ML⁻¹T⁻²] |
| 13. | Impulse | Force × Time | [MLT⁻¹] |
| 14. | Torque | Force × Distance (perpendicular) | [ML²T⁻²] |
| 15. | Stress | Force ÷ Area | [ML⁻¹T⁻²] |
| 16. | Strain | Change in Length ÷ Original Length | No unit or dimension |
| 17. | Modulus of Elasticity | Stress ÷ Strain | [ML⁻¹T⁻²] |
| 18. | Surface Tension | Force ÷ Length | [MT⁻²] |
| 19. | Gravitational Constant (G) | (Force × Distance²) ÷ (Mass × Mass) | [M⁻¹L³T⁻²] |
| 20. | Gravitational Field Strength | Gravity Force ÷ Mass | [LT⁻²] |
| 21. | Gravitational Potential | Work ÷ Mass | [L²T⁻²] |
| 22. | Spring Constant (Force constant) | Force ÷ Stretch or Compression (length) | [MT⁻²] |
| 23. | Frequency | 1 ÷ Time (Number of cycles per second) | [T⁻¹] |
| 24. | Angle (in radians) | Arc ÷ Radius | No dimension |
| 25. | Angular Velocity | Angle ÷ Time | [T⁻¹] |
| 26. | Angular Acceleration | Angular Velocity ÷ Time | [T⁻²] |
| 27. | Moment of Inertia | Mass × Distance² | [ML²] |
| 28. | Angular Momentum | Moment of Inertia × Angular Velocity | [ML²T⁻¹] |
| 29. | Specific Heat | Heat Energy ÷ (Mass × Temperature Change) | [L²T⁻²θ⁻¹] (θ = temperature) |
Explanation in Simple Words:
- Length, Mass, and Time are the most basic physical quantities.
- When we combine them in different ways, we get derived quantities like speed, force, energy, etc.
- We use formulas to find their values.
- Dimensional formulas help us understand what basic units make up a quantity.
FAQ
What is the SI Unit System?
The SI Unit System is a way of measuring things using a standard set of units. It helps everyone in the world use the same language for measuring, like meters for length or kilograms for weight.
Why do we use the SI Unit System?
We use the SI Unit System so that everyone can understand each other. Whether you are in India or America, if you say “5 meters,” it means the same thing. It avoids confusion.
What does “SI” stand for?
“SI” stands for “Système International,” which is French for “International System.” It is the short name for the global system of units.
Who uses the SI Unit System?
Almost every country in the world uses the SI Unit System. Scientists, teachers, engineers, and even school children use it daily.
Is the SI Unit System easy to learn?
Yes, it is very easy to learn. Once you know a few basic units, you can measure almost anything — distance, time, weight, and even electricity.Can I use other units instead of SI units?
You can, but SI units are the most accepted and trusted around the world. So, it’s best to use SI units whenever possible.

