Table of Contents
Difference Between Ideal and Practical Transformer
When it comes to learning about transformers, two terms often pop up: ideal transformer and practical transformer. They sound similar, but there’s a big difference between them. Let’s explore it in a way that’s easy to understand.
What is a Transformer?
A transformer is an electrical device that transfers electrical energy from one circuit to another through the process of electromagnetic induction. It works on the principle of mutual induction, where a changing current in one coil (the primary winding) generates a changing magnetic field, which then induces a voltage in another coil (the secondary winding).
Transformers are mainly used to increase (step up) or decrease (step down) voltage levels in power systems without changing the frequency. They are essential for the efficient transmission and distribution of electricity over long distances, as high-voltage transmission reduces energy losses.
Key parts of a transformer include:
- Primary Winding: The coil is connected to the input voltage source.
- Secondary Winding: The coil is connected to the output load.
- Core: Made of laminated soft iron to provide a path for magnetic flux and reduce core losses.
1. What is an Ideal Transformer?
Imagine a perfect machine that takes in electrical power and gives out the same amount — no heat, no losses, no waste. That’s an ideal transformer. It’s 100% efficient and works without any flaws. In theory, it has:
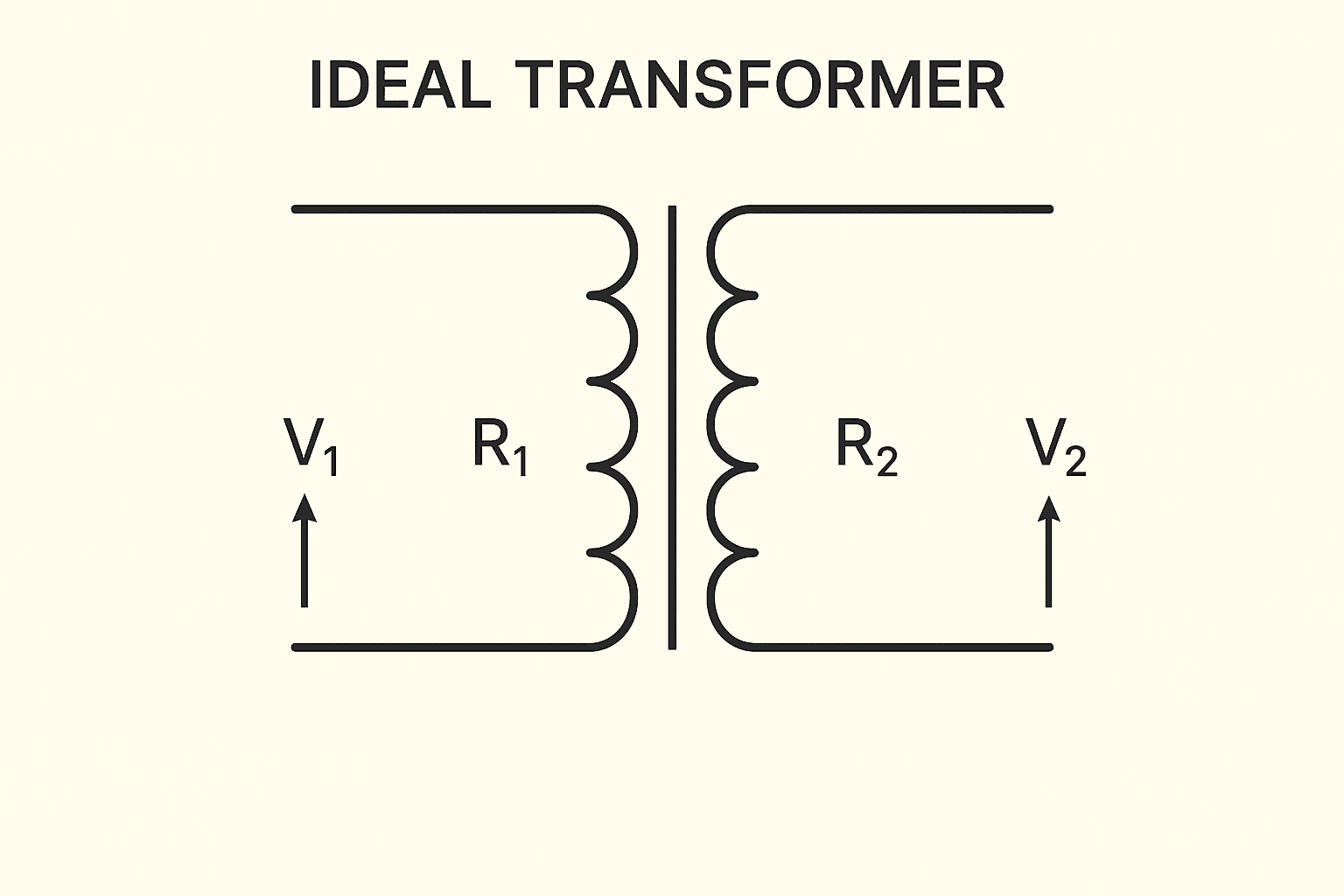
- Zero winding resistance — so no heat loss in the wires, meaning all the electrical energy passes through without being turned into unwanted heat.
- No flux leakage — every bit of magnetic energy created in one winding reaches the other winding, ensuring perfect energy transfer.
- Perfect core — never gets saturated, no matter how much magnetic flux passes through, so it operates smoothly at all times.
- No-load power waste — the tiny current it uses at no-load is only for creating the magnetic field, and it doesn’t consume any real power for this.
- 100% efficiency — every single watt you put in comes out on the other side with no reduction at all.
In simpler words, it’s like having a water pipe that delivers exactly the same amount of water at the other end without a single drop leaking or evaporating. Sounds perfect, right? Well… there’s a catch — it doesn’t exist in the real world.
Ideal Transformer Characteristics
An ideal transformer is a theoretical model that operates with 100% efficiency, meaning there are no energy losses of any kind. Although no real transformer is truly ideal, studying its characteristics simplifies calculations and provides a foundation for analyzing practical transformers.
Key Characteristics of an Ideal Transformer:
- No Energy Losses:
- There are no core losses (hysteresis or eddy current) and no copper losses (I²R losses) in the windings.
- All the power supplied to the primary winding is perfectly transferred to the secondary winding without any loss.
- Perfect Magnetic Coupling:
- All the magnetic flux generated in the primary winding links completely with the secondary winding.
- There is no leakage flux.
- Zero Resistance Windings:
- Windings are assumed to have no electrical resistance.
- This eliminates any voltage drops within the windings.
- No Leakage Reactance:
- The leakage inductance of the windings is zero, ensuring the entire flux links both windings.
- Constant Frequency:
- The transformer operates at a constant frequency, which remains the same in both the primary and secondary windings.
- Voltage and Current Relationship:
- The voltage ratio is directly proportional to the turns ratio of the windings.
- 100% Efficiency:
- Input power equals output power ().
Ideal Transformer Phasor Diagram
An ideal transformer is a simplified model of a transformer in which there are no energy losses. This means:
- No winding resistance.
- No leakage flux.
- No core losses (like hysteresis or eddy currents).
- Perfect magnetic coupling between primary and secondary windings.
In an ideal transformer, the input power equals the output power:
V1I1=V2I2
Where:
- V1 and I1 are the primary voltage and current.
- V2 and I2 are the secondary voltage and current.
Phasor Diagram Explanation:
- Reference Voltage: We usually take the primary voltage V1 as the reference phasor (drawn horizontally).
- Primary Current: The primary current I1 lags the voltage by the load power factor angle ϕ\phi.
- Secondary Voltage: In an ideal transformer, V2 is exactly in phase with V1 if the load is purely resistive.
- Turns Ratio Relationship:
V1/V2=N1/N2=I2/I1
Drawing the Phasor Diagram:
- Draw a horizontal line for V1 as the reference.
- Mark I1 lagging by ϕ\phi (for inductive loads) or leading (for capacitive loads).
- Draw V2 either in phase with V1 or shifted according to the load type.
- Indicate I2 in phase with I1 (for the ideal case) but with a different magnitude depending on the turns ratio.
2. What is a Practical Transformer?
This is the transformer we actually use in daily life, the kind that powers our homes, industries, and countless devices. It’s built to be as close to the ideal one as possible, but, like all real-world machines, it has some natural limitations that come from physical materials and operating conditions:
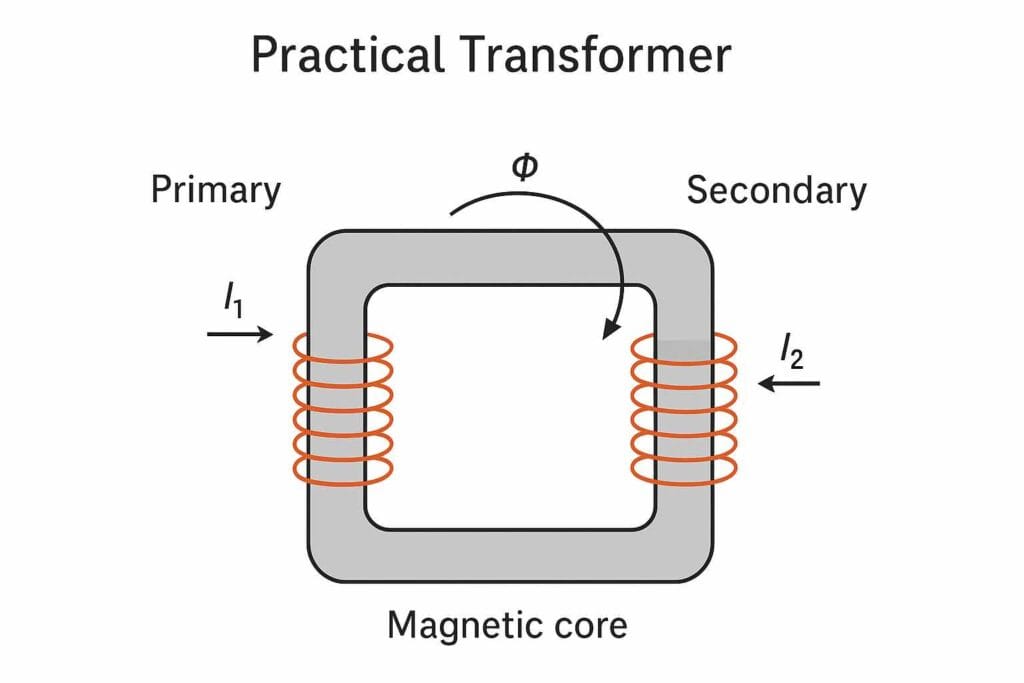
- Small winding resistance — the wires used in the coils have a little electrical resistance, which means some electrical energy is turned into heat, leading to what we call copper loss. While this is minimized with good design, it can’t be fully eliminated.
- Some flux leakage — not all the magnetic field generated in the primary winding passes through the core to the secondary winding. A small portion escapes, which slightly reduces efficiency.
- Core limits — the iron or steel core has a maximum amount of magnetic flux it can carry. At high loads, the core can reach a saturation point, which affects performance.
- Extra no-load current — even when the transformer isn’t supplying any load, it still draws a small amount of current to keep the magnetic field alive and to cover iron losses caused by hysteresis and eddy currents in the core.
- High but not perfect efficiency — practical transformers often achieve impressive efficiency, typically between 90% and 99%, but never the ideal 100%. This small gap comes from unavoidable energy losses.
Practical Transformer Characteristics
A practical transformer is a real-world electrical device that transfers electrical energy between two or more circuits using electromagnetic induction. Unlike the ideal transformer, which is a simplified theoretical model, the practical transformer includes certain losses and inefficiencies that occur in real operation. These characteristics make it more realistic but also slightly less efficient.
Key Characteristics:
- Core Losses: Practical transformers experience core losses, also called iron losses, due to hysteresis and eddy currents in the core. These losses occur whenever the transformer is energized, regardless of load.
- Copper Losses: The windings in a practical transformer have electrical resistance, which causes heat generation when current flows. This leads to copper losses, proportional to the square of the load current.
- Leakage Flux: Not all the magnetic flux generated by the primary winding links with the secondary winding. Some flux ‘leaks’ into the surroundings, reducing efficiency.
- Magnetizing Current: A small amount of current is required to magnetize the core, even with no load connected. This is absent in an ideal transformer.
- Voltage Regulation: In a practical transformer, the output voltage slightly decreases when the load increases due to internal impedance.
- Efficiency: Practical transformers are highly efficient but not 100%. Large power transformers can reach efficiencies above 98%, but small losses always remain.
Practical Transformer Phasor Diagram
A phasor diagram is a visual tool used to represent the phase relationships between different voltage and current waveforms in a transformer. For a practical transformer, unlike an ideal one, we must consider the real-world imperfections like winding resistance, leakage reactance, and core losses. These imperfections cause voltage drops and slight phase shifts, making the phasor diagram more complex.
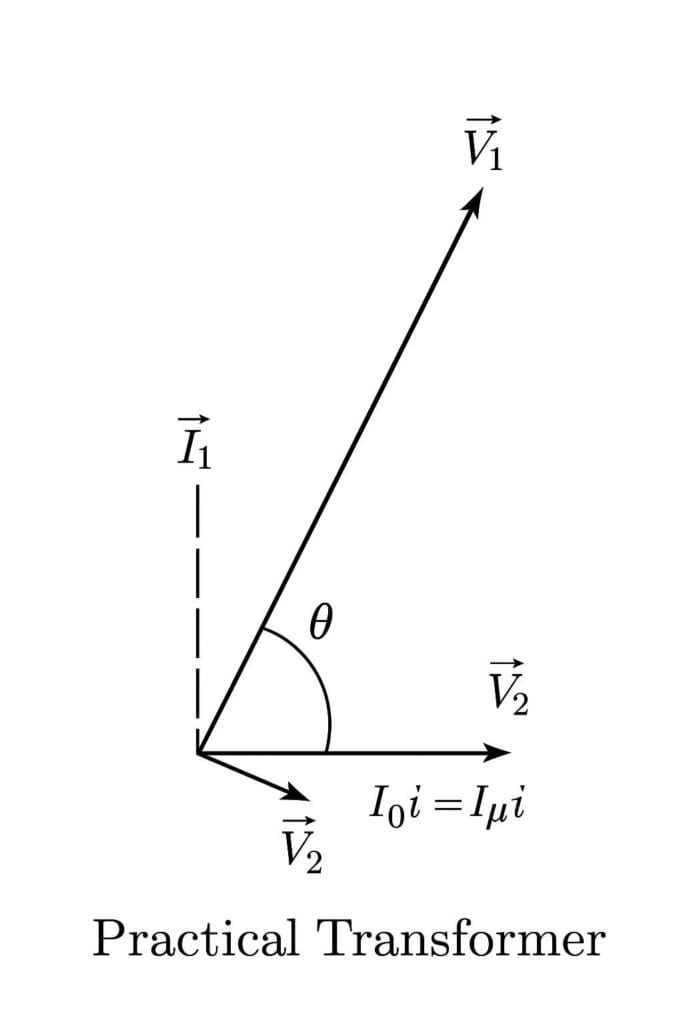
Steps to Draw a Practical Transformer Phasor Diagram
1. Start with the applied voltage (V1)
Draw the primary supply voltage V1 horizontally as the reference phasor.
2. Add the no-load current (I0)
The no-load current is small and lags behind V1 by an angle close to 90° due to the magnetizing component. It has two parts:
- Im: Magnetizing current (lags by 90°)
- Iw: Core loss component (in phase with V1)
3. Include the load current (I2′)
Refer the secondary current to the primary side (I2′) using the turns ratio. The direction of I2′ depends on the load power factor.
4. Add voltage drops in the winding
Account for the primary winding resistance (R1) and leakage reactance (X1):
- IR drop: In phase with current
- IX drop: 90° ahead of current
5. Draw the induced EMF (E1)
Subtract the voltage drops (IR1 and IX1) from V1 to get the induced EMF E1.
6. Relate primary and secondary
The induced EMF E1 is linked to the secondary induced EMF E2 by the turns ratio. On the secondary side, similar drops occur due to R2 and X2.
Key Differences from the Ideal Transformer Phasor Diagram
- Voltage drops in both primary and secondary windings
- Phase shifts due to leakage reactance and winding resistance
- Core loss representation through Iw component
- Larger overall phase difference between voltage and current
Difference Between Ideal and Practical Transformer
Here’s an expanded comparison table with more details and additional points for better understanding:

| Feature | Ideal Transformer | Practical Transformer |
|---|---|---|
| Definition | A theoretical transformer with no losses and perfect operation. | A real-world transformer that experiences certain inefficiencies. |
| Efficiency | 100% efficient, with all input power transferred to output. | Less than 100% due to copper losses, core losses, and stray losses. |
| Winding Resistance | Zero resistance in both primary and secondary windings. | Small but measurable winding resistance causes power loss. |
| Leakage Flux | No leakage flux; all magnetic flux perfectly links both windings. | Some leakage flux exists, leading to reduced energy transfer efficiency. |
| Core Losses | No hysteresis or eddy current losses in the core. | Core losses occur due to hysteresis and eddy currents in the core material. |
| Voltage Regulation | Perfect regulation; output voltage remains constant regardless of load. | Voltage drops slightly under load due to winding resistance and leakage reactance. |
| Heating | No heat generation at all. | Heat is produced due to copper losses and magnetic core losses. |
| Physical Size | Can be infinitely small in theoretical design. | Has a definite physical size based on power rating and insulation requirements. |
| Cost | Not applicable, as it is purely a theoretical concept. | Real transformers incur manufacturing, labor, and material costs. |
| Maintenance | No maintenance needed. | Requires periodic inspection and maintenance to ensure optimal performance. |
| Overload Handling | Can handle any load without overheating or performance drop. | Overloading can cause excessive heating and reduce lifespan. |
| Lifespan | Infinite, as there is no wear and tear. | Limited lifespan due to insulation degradation and mechanical stress. |
FAQ
What is the main difference between an ideal and a practical transformer?
An ideal transformer has no losses and operates with 100% efficiency, whereas a practical transformer experiences losses such as copper loss, core loss, and leakage flux.
Can an ideal transformer exist in reality?
No. An ideal transformer is purely theoretical, used for simplification in analysis and design.
Why do practical transformers have losses?
They are built from real materials with resistance and imperfect magnetic properties, which lead to energy losses during operation.
Which is more efficient: an ideal or a practical transformer?
An ideal transformer is 100% efficient in theory. A practical transformer’s efficiency is slightly less due to unavoidable losses.

