Parallel Plate Capacitor: definition, formula, types, principle

Definition of Parallel Plate Capacitor

A parallel plate capacitor is a device made of two flat, conductive plates placed parallel to each other with a small gap between them. This gap is usually filled with air or a material called a dielectric.

When we connect a battery or voltage source across the plates, one plate gets positive charge, and the other gets negative charge. This setup stores electric energy in the form of an electric field between the plates.

✅ Key Features:

• Plates: Two flat metal plates.
• Distance: Small space d between the plates.
• Area: Each plate has area A.
• Dielectric: The material between the plates, which affects how much charge the capacitor can hold.

📐 Capacitance Formula:

C = (ε0 × εr × A) / d

Where:

• C = capacitance (in farads)
• ε0 = permittivity of free space
• εr = relative permittivity of the dielectric
• A = area of each plate
• d = distance between the plates

capacitor formula

Let’s try to understand this in a simple way.

We already know that capacitance tells us how much electric charge a capacitor can hold for a given voltage. The basic formula is:

C = Q / V

This means:

• C is the capacitance,
• Q is the charge,
• V is the voltage.

But sometimes, we don’t just want to use electrical values. We want to know the capacitance based on the shape and material of the capacitor. The most common type is the parallel-plate capacitor.

capacitor working principle for beginners

You have two flat plates.

• Each plate has an area A (in square metres).
• They are kept apart by a small distance d (in metres).
• The space between the plates is filled with a material (called a dielectric).
• This material has a special property called relative permittivity, written as ε_r.

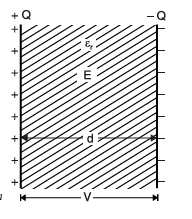
Now, when we apply a voltage V across the plates, one plate becomes positively charged (+Q) and the other negatively charged (–Q). This is the setup where we use the parallel plate capacitor formula.

The electric field between the plates is almost the same everywhere — like a straight line from one plate to the other.

parallel plate capacitor formula:

Let’s understand the process using the parallel plate capacitor formula:

The electric flux density (D) between the plates is:

D = Q / A

The electric field (E) between the plates is:

E = V / d

Now comes a key relationship used in the parallel plate capacitor formula:

D=ε0​×εr​×E

Substitute the expressions:

Q/A=ε0×εr×V/d​

Rearranging this to find the capacitance C=Q/V we get:

Now, there’s a special relationship between D, E, and the properties of the material:

D = ε₀ × ε_r × E

So, putting it all together:

Q / A = ε₀ × ε_r × V / d

Let’s rearrange this to find C = Q / V:

So finally, the capacitance of the parallel-plate capacitor is:

C = (ε₀ × ε_r × A) / d

This is the formula for capacitance in a medium.

If there is air between the plates (or vacuum), then ε_r = 1, and the formula becomes:

From the air-only parallel plate capacitor formula, we can also rearrange to find:

ε0​=C×d​/A

This is the standard parallel plate capacitor formula when a dielectric medium is used.

C=ε0​×εr​×A​/d

capacitor key points:

Capacitance increases when:

The area A is large.

The material has higher ε_r.

Capacitance decreases when:

The distance d between the plates is more.

ε_r is the relative permittivity of the material between the plates.

You can also find ε₀, the permittivity of free space, from the formula in air: ε₀ = (C × d) / A (Unit: farad per metre → F/m)

Parallel-Plate Capacitor with Composite Medium – Simple Explanation

Let’s consider a special case of the parallel plate capacitor formula where three different materials fill the gap between the plates.

Now, usually, this space is filled with air or just one kind of material (called a dielectric). But in this case, we are filling the space with three different materials — each with its own thickness and ability to store electric energy.

Let’s call:

• Thicknesses of the materials: d₁, d₂, and d₃
• Their strength to hold electric charge (relative permittivity): εᵣ₁, εᵣ₂, and εᵣ₃

Even though these materials are different, the electric flux (let’s call it D) is the same in all of them. It’s like how the same amount of water flows through different pipes — the pressure might change, but the flow stays the same.

Now, the electric field (E) inside each material is different. Why? Because each material reacts differently to the electric charge.

We find each electric field using this simple formula:

E = D / (ε₀ × εᵣ)

So for each material:

• E₁ = D / (ε₀ × εᵣ₁)
• E₂ = D / (ε₀ × εᵣ₂)
• E₃ = D / (ε₀ × εᵣ₃)

Here, ε₀ is a fixed value, known as the permittivity of free space.

The overall voltage is the sum of voltages across each layer. From this, we can derive the parallel plate capacitor formula for layered dielectrics using series combination rules.

🔌 Voltage Across the Capacitor

The total voltage (V) across the plates is the sum of voltages across each material:

V = V₁ + V₂ + V₃

And since Voltage = Electric field × Distance, we write:

V = E₁ × d₁ + E₂ × d₂ + E₃ × d₃

That means the total push (voltage) is made up of the push across each layer.

🧮 Capacitance of the Composite Capacitor

Now, let’s find the capacitance (C) — the power of the capacitor to store charge.

We already know:

Capacitance, C = Charge (Q) / Voltage (V)

After putting everything together (as shown in the formulas), we get:

C = ε₀ × A / [d₁/εᵣ₁ + d₂/εᵣ₂ + d₃/εᵣ₃]

Where:

• A is the area of the plates
• d₁, d₂, d₃ are the thicknesses of the layers
• εᵣ₁, εᵣ₂, εᵣ₃ are their relative permittivities

This is the final formula that helps us calculate how much charge this special capacitor can hold.

🧠 Final Thought

• A capacitor can be filled with different materials, and each one affects how it works.
• The electric field changes inside each material, but the electric flux stays the same.
• The total voltage is just the sum of each part.
• And we can find the capacitance using a nice, simple formula.
  
  

Capacitor with Air and Dielectric

Let’s imagine you have two flat metal plates. These plates are placed a little distance apart — let’s call that distance d metres. This setup is called a parallel plate capacitor.

Now, between these two plates, there is usually air. But sometimes, we add another material in between. This special material is called a dielectric. It helps the capacitor store more electric charge.

Let’s now understand two different situations:

(i) When the space is partly air and partly dielectric

Suppose between the two plates, part of the space is filled with air and the other part is filled with a dielectric material.

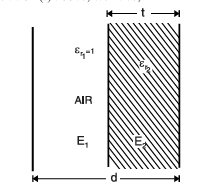
• The total gap between the plates is d metres.
• The dielectric material takes up t metres of space.
• So, the remaining space (which is just air) will be (d − t) metres.
• Let’s say the dielectric material has a relative permittivity (how well it stores electric charge) of εr.

The capacitance (ability to store electric charge) of this setup becomes:

C = (ε₀ × A) / [(d − t) + (t / εr)]

Where:

• C is the capacitance.
• ε₀ is a constant value (electric permittivity of free space).
• A is the area of the plates.
• d − t is the thickness of the air part.
• t is the thickness of the dielectric.

(ii) When a dielectric slab is fully inserted between the plates

Now imagine you have just air between the plates. But then, you gently slide in a dielectric slab of thickness t metres. The rest of the space still has air.

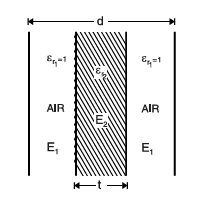
This situation is similar to the first one. Part of the space is filled with the slab (dielectric), and part is still air.

The capacitance in this case also follows the same formula:

C = (ε₀ × A) / [(d − t) + (t / εr)]

Special Cases of a Parallel-Plate Capacitor

We already know that the capacitance of a capacitor depends on three things:

• The area of its plates
• The thickness of the material (called dielectric) between the plates
• The type of dielectric used (its relative permittivity, written as εr)

Let’s now look at two special cases to understand this better.

Case 1: Two Different Dielectrics Side by Side

Imagine a capacitor where the plate is divided into two parts:

• One part (area A₁) has air between the plates.
• The other part (area A₂) has a dielectric material with relative permittivity εr.

Even though both parts have the same thickness d, they have different materials. So, this setup acts like two capacitors placed side by side (in parallel).

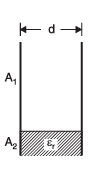
The capacitance of the air part is:
C₁ = ε₀ A₁ / d

The capacitance of the dielectric part is:
C₂ = ε₀ εr A₂ / d

So, the total capacitance is:
C = C₁ + C₂

Case 2: Two Dielectrics Placed One After Another

In this case, the plate is still divided into two areas:

• The first part (area A₁) has only air between the plates, with a thickness d.
• The second part (area A₂) has two layers between the plates:
  • A dielectric material (relative permittivity εr) of thickness t
  • Air filling the remaining thickness (d – t)

This also acts like two capacitors placed in parallel.

The capacitance of the air-only part is:
C₁ = ε₀ A₁ / d

The capacitance of the two-layer part is:
C₂ = ε₀ εr A₂ / [d – t + (t / εr)]

So, the total capacitance is:
C = C₁ + C₂

multiplate capacitor explained

If we want a capacitor to store more charge, we need to make its capacitance bigger. The easiest way to do this is by using larger plates. But making the plates bigger also makes the capacitor very large and bulky, which is not always practical.

To solve this problem, we use something smart called a multiplate capacitor.

🧩 What is a Multiplate Capacitor?

A multiplate capacitor is made by stacking many thin metal plates and thin insulating sheets (called dielectrics) one after the other. The metal sheets are the plates, and the thin sheets between them are the dielectric materials.

• All the odd-numbered plates (1st, 3rd, 5th, etc.) are joined together to make one terminal, called T1.
• All the even-numbered plates (2nd, 4th, 6th, etc.) are joined to form the second terminal, called T2.

This clever design helps us pack more plate area in a smaller space.

⚡ Why is This Design Helpful?

Let’s understand it with an example. If we use 7 plates, we actually create 6 small capacitors side by side (in parallel). That means the total capacitance becomes 6 times more than just using two plates.

So, if we use n plates, the number of capacitors formed will be (n – 1).

This means the total capacitance increases a lot without making the capacitor too big!

🧮 multiplate capacitor formula

If:

• n = total number of plates
• A = area of each plate
• d = distance between two plates
• ε₀ = permittivity of free space
• εᵣ = relative permittivity (how well the material between plates stores electric energy)

Then, the capacitance is given by:

C = ε₀ × εᵣ × A × (n − 1) / d

This shows that when we add more plates, the area becomes (n – 1) × A, so the capacitance increases.

📝 A Few More Tips

• We can also increase capacitance by:
  • Using a better dielectric material (with high εᵣ)
  • Reducing the distance between the plates
• But using high-quality dielectric can be costly, and reducing the gap too much can break the insulation, so we must be careful.

Variable Air Capacitor – Explained Simply

A Variable Air Capacitor is a special kind of capacitor that you can adjust or change to increase or decrease its strength.

Imagine two sets of shiny metal plates.

• One set is fixed (it doesn’t move).
• The other set can move in and out by turning a knob or shaft.

These plates do not touch each other. They are kept apart, and the space between them is filled with air – that’s why it’s called an air capacitor.

Now, here’s the fun part:

• When the moving plates slide into the spaces between the fixed plates, more plate area is shared between them.
• This makes the capacitor stronger – we say its capacitance increases.
• When the moving plates slide out, less area is shared, and the capacitance becomes smaller.

👉 So, by turning the shaft, we can change how much the plates overlap — and that’s how we control the capacitance.

uses of variable air capacitor

Variable air capacitors are often used in radios. By changing the capacitance, we can tune the radio to different stations.

Capacitance Range:

• The smallest value is close to zero.
• The biggest value can go up to about 4000 pF (that’s a tiny unit of measurement for capacitance).

Simple Formula:

The capacitance depends on:

• How much the plates overlap,
• How far apart they are,
• And the material between them (in this case, it’s just air).

🌟 In short:

A Variable Air Capacitor is like a smart knob that lets us tune or adjust how much electric energy it can store, just by moving some metal plates in and out — no wires, no batteries, just clever design!

Air Capacitor with a Dielectric Slab – Explained Simply

Imagine you have two flat metal plates. These plates are like slices of bread, and there’s only air between them. This setup is called an air capacitor. The size of each plate is 1500 cm², and the gap between them is 5 mm.

Now, let’s say you slide a special piece of material (called a dielectric slab) between these two plates. This slab is 2 mm thick, covers the whole area of the plates, and has something called relative permittivity of 3. That just means it can store more electric charge than air can.

But here’s the twist: when you add this slab, the capacitor becomes stronger. It stores more charge than before. But we don’t want that — we want to keep the original strength, the same as it was with just air.

So how do we fix it?

We move the plates farther apart. But not too far — just the right amount to cancel out the effect of the slab.

Problem (in simple words):

We have a capacitor made up of two flat plates.

• Each plate is 0.01 square meter in size.
• There is a 1 mm thick layer of a material (dielectric) between them.
• The voltage (potential difference) across the plates is 10,000 volts (10 kV).
• The capacitance of this setup is 300 pF (picoFarads).

Now, let’s find out the following four things:

1. Total electric flux
2. Electric flux density
3. Potential gradient
4. Relative permittivity of the dielectric material

Given values:

• Capacitance, C = 300 × 10⁻¹² F
• Voltage, V = 10,000 V = 10⁴ V
• Area of plates, A = 0.01 m²
• Distance between plates, d = 1 mm = 0.001 m
• Vacuum permittivity, ε₀ = 8.854 × 10⁻¹² F/m

Step-by-step Solution:

(i) Total electric flux (Q):

We use the formula:
Q = C × V

Put the values:
Q = (300 × 10⁻¹²) × (10⁴)
Q = 3 × 10⁻⁶ coulombs
👉 So, the total electric flux is 3 microcoulombs (3 μC)

(ii) Electric flux density (D):

We use the formula:
D = Q / A

Put the values:
D = (3 × 10⁻⁶ C) / (0.01 m²)
D = 3 × 10⁻⁴ C/m²
👉 So, the electric flux density is 3 × 10⁻⁴ C/m²

(iii) Potential gradient (E):

This is also called the electric field.
We use the formula:
E = V / d

Put the values:
E = 10⁴ V / 0.001 m
E = 1 × 10⁷ V/m
👉 So, the potential gradient is 10⁷ volts per meter

(iv) Relative permittivity (εᵣ):

We use the formula:
D = ε₀ × εᵣ × E
Rearrange to find εᵣ:
εᵣ = D / (ε₀ × E)

Put the values:
εᵣ = (3 × 10⁻⁴) / (8.854 × 10⁻¹² × 10⁷)
εᵣ ≈ 3.39
👉 So, the relative permittivity of the material is about 3.39

✅ Final Answers:

1. Electric flux (Q): 3 μC
2. Electric flux density (D): 3 × 10⁻⁴ C/m²
3. Potential gradient (E): 10⁷ V/m
4. Relative permittivity (εᵣ): 3.39

FAQ