capacitors in series and parallel: Formula, exam useful fact

​

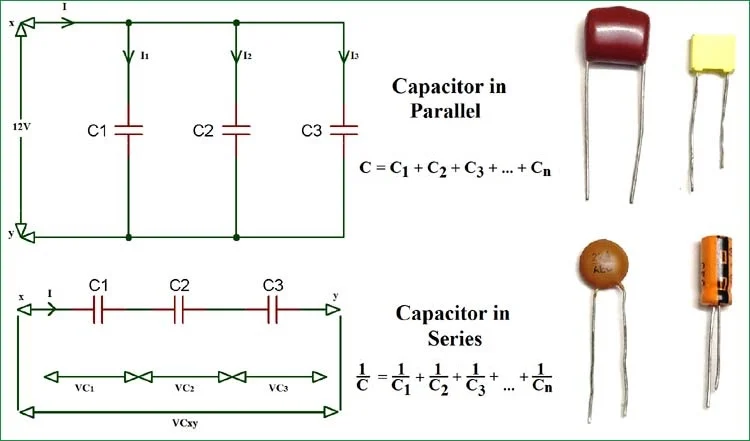
Capacitors in Series and parallel

Let’s imagine you have three capacitors — we’ll call them C₁, C₂, and C₃.
Now, we connect them one after another, like links in a chain. This is called a series connection.

When we apply a voltage V across this whole chain, something interesting happens:

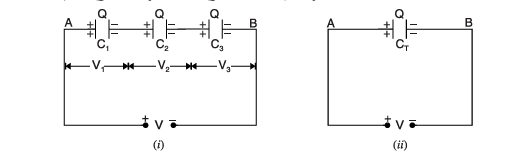
• Each capacitor gets the same charge (Q).
• But the voltage across each one is different.
  That means the first capacitor gets V₁, the second one gets V₂, and the third one gets V₃.
  And together, they add up to the total voltage:
  V = V₁ + V₂ + V₃

Now, remember a simple rule:
Q = C × V (Charge = Capacitance × Voltage)

If we rearrange this, we get:
V = Q ÷ C

So for each capacitor:

• V₁ = Q ÷ C₁
• V₂ = Q ÷ C₂
• V₃ = Q ÷ C₃

Adding them gives:

V = Q × (1/C₁ + 1/C₂ + 1/C₃)

Let’s bring the Q to the other side:

1/CT = 1/C₁ + 1/C₂ + 1/C₃

This is the formula for total or equivalent capacitance when capacitors are connected in series:

“1/CT = 1/C₁ + 1/C₂ + 1/C₃”

🔹 Special Case: Only Two Capacitors in Series

Sometimes, we only have two capacitors — C₁ and C₂. Then the formula becomes:

“1/CT = 1/C₁ + 1/C₂”

Or you can directly write:

“CT = (C₁ × C₂) ÷ (C₁ + C₂)”

When we need to handle a higher voltage in a circuit—more than what a single capacitor can take—we use more than one capacitor and connect them in a line, one after another. This is called a series connection.

In this case, the total value of the capacitors becomes a bit different. We don’t simply add them. Instead, we use a special formula.

“1 / CT = 1 / C1 + 1 / C2 + 1 / C3 + …”

Here,
CT means Total Capacitance
C1, C2, C3… are the values of each capacitor in the series.

Now, one important thing to remember:

• When capacitors are connected in series, they don’t all get the same voltage.
• Smaller capacitors get more voltage, and bigger ones get less.
• If one capacitor gets too much voltage, it can break or stop working.

That’s why we must be careful. To be safe, it’s better if all the capacitors in the series are equal in value.

So always remember:
Using capacitors in series helps us handle high voltage, but only when we match them properly.

🔹 What Actually Happens Inside?

When you connect the capacitors in series and apply voltage:

• Electrons move just once through the whole path.
• That’s why the same amount of charge reaches every capacitor.
• The current stays the same through the path too.

So even though the voltages may be different, the charge Q is the same on all the capacitors.

Capacitors in Parallel

Let’s imagine you have three capacitors. They are named C1, C2, and C3. Each one has its own value of capacitance, like how different cups can hold different amounts of water.

Now, suppose we connect all three capacitors side by side, with their ends joined together. This is called a parallel connection. We also connect them to a battery that gives a voltage of V volts.

In this setup:

• The voltage (V) across each capacitor stays the same.
• But the charge stored in each one is different, depending on how big or small each capacitor is.

So what happens to the total charge?

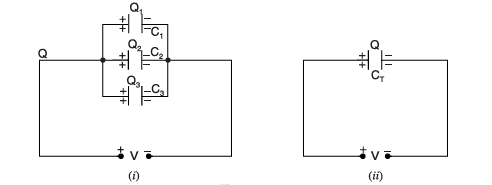
Let’s say:

• The charge on capacitor C1 is Q1 = C1 × V
• The charge on capacitor C2 is Q2 = C2 × V
• The charge on capacitor C3 is Q3 = C3 × V

To find the total charge (Q) stored in the whole system, we just add the charges:

Q = Q1 + Q2 + Q3
Q = C1 × V + C2 × V + C3 × V
Q = V × (C1 + C2 + C3)

Now, total capacitance means how much charge is stored per volt. So:

Total capacitance (CT) = Q / V = C1 + C2 + C3

✅ So, Capacitors in Parallel :

Total capacitance is the sum of individual capacitances.

CT = C1 + C2 + C3

That’s it!

📌 Why connect capacitors in parallel?

Sometimes, a single capacitor doesn’t have a big enough value. So, we join them in parallel to make a bigger total capacitance. This way, the circuit can store more charge easily.

Joining Two Charged Capacitors in Parallel

Imagine you have two balloons. One is filled with a lot of air, and the other has just a little. Now, if you connect them with a pipe, air will move from the fuller balloon to the emptier one until both have the same amount of air. This is exactly what happens when we connect two charged capacitors.

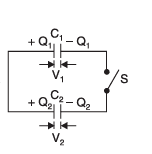
Let’s say:

• One capacitor has capacitance C₁ and is charged to a voltage V₁
• The other has capacitance C₂ and is charged to voltage V₂

At first, both capacitors hold different amounts of electric charge:

• Q₁ = C₁ × V₁
• Q₂ = C₂ × V₂

Now, when we close the switch and connect them together:

• Charge starts to flow from the capacitor with higher voltage to the one with lower voltage
• This flow continues until both have the same voltage
• That final equal voltage is called the common potential (V)

We can find this common potential using a simple formula: Common Potential V=C1V1+C2V2/C1+C2

This just means:

• Add the total charge (C₁V₁ + C₂V₂)
• Divide it by the total capacitance (C₁ + C₂)

📘 Some Important Points of Capacitors in Parallel

1. Charge is not lost: The total amount of charge stays the same. One capacitor gives charge, and the other receives it. It’s like sharing, not losing.
2. They become parallel: Once the switch is closed, the capacitors are connected side by side, just like parallel wires.
3. Equal voltage: After connection, both capacitors reach the same voltage (common potential). But the charge on each depends on their size. A bigger capacitor will hold more charge, just like a bigger jar holds more water.
4. Some energy is lost: Even though charge is shared, some energy disappears as heat. This heat comes from the moving charge rubbing through the wire, just like how your hands get warm when you rub them fast.

Problem Statement

Two capacitors are given:

• One is 4 microfarads (µF)
• The other is 6 microfarads (µF)

First, they are connected in series with a battery of 250 volts.

Then, they are removed from the battery and joined in parallel with each other.

We need to find:

1. The new voltage (p.d.) across them after connecting in parallel
2. The charge on each capacitor in this new setup

Step-by-Step Easy Solution

Step 1: Capacitors in Series

When we connect capacitors in series, the charge on each is the same.

But the voltage is shared between them depending on their size (capacitance).
A small capacitor gets more voltage, a large one gets less.

Let’s find the voltage across each:

We use the rule:

In series, voltage is divided opposite to the size (capacitance).

So,

• Voltage across 4 µF = (6 / (4 + 6)) × 250 = 150 V
• Voltage across 6 µF = (4 / (4 + 6)) × 250 = 100 V

Now let’s find the charge on either capacitor.

We use the formula:

Q = C × V

So,

• Charge on 4 µF = 4 × 10⁻⁶ × 150 = 0.0006 C
  This is the same charge for both because they are in series.

So total charge = 0.0006 C + 0.0006 C = 0.0012 C

Step 2: Capacitors in Parallel

Now, they are disconnected from the battery and connected in parallel.

In parallel:

• They both get the same voltage
• The charge is shared based on their size

First, find the total size (capacitance) when in parallel:

• Total C = 4 + 6 = 10 µF

We already know the total charge = 0.0012 C

Now use this to find the new common voltage (V):

V = Q / C = 0.0012 / (10 × 10⁻⁶) = 120 V

Step 3: Find the Charge on Each Capacitor in Parallel

Now that we know the voltage is 120 V, we find the charge using Q = C × V again:

• For 4 µF:
  Q = 4 × 10⁻⁶ × 120 = 480 µC
• For 6 µF:
  Q = 6 × 10⁻⁶ × 120 = 720 µC

Energy Stored in a Capacitor

When we charge a capacitor, we are simply moving tiny particles called electrons from one plate of the capacitor to the other. But this is not as easy as it sounds. It takes effort (energy) to push these electrons, because they don’t want to move easily. They are moving against a force.

This energy that we use to push the electrons doesn’t disappear. It gets stored inside the capacitor, in the electric field created between the plates. This field lives in the space between the plates, which is filled with a special material called a dielectric.

Now, imagine a capacitor with a size of C farads connected to a battery of V volts.

At the start, the capacitor is empty—there’s no charge. As we slowly add charge (let’s call the charge Q) to the plates, the voltage between the plates starts to rise.

As we keep charging it, more and more energy is needed. All of this energy goes into building that electric field.

When the capacitor is fully charged, the total energy stored in it is given by a very simple and useful formula:

✅ Energy Stored in a Capacitor formula =

1/2×C×V2

Or, 1/2×Q×V

Or, {Q^2}{2C}

You can use whichever one is most helpful, depending on what values you know.

🔋 What Happens to This Energy?

• The capacitor does not waste this energy.
• It doesn’t burn it, and it doesn’t use it up like a heater or a light bulb.
• It simply stores it—like a balloon holding air.

Later, when the capacitor is discharged, this energy is released back, just like a balloon letting air out.

Energy Density of Electric Field 🌟

What is it?
The energy density of an electric field means how much energy is stored in a certain space where the electric field exists. Simply put, it is the energy stored in each unit of volume.

✅ Easy Definition:

Energy Density (u) =
Energy Stored ÷ Volume of the Electric Field

So, whenever there is an electric field — even if we can’t see it — some energy is quietly stored there. This energy is not spread all over but is packed into the space where the electric field is active.

🧪 Let’s Understand with an Example:

Imagine a parallel plate capacitor — like two big flat plates facing each other with a small gap between them.

• These plates are charged.
• One has extra electrons (negative) and the other is missing some (positive).
• This setup creates an electric field between the plates.

As we charge the plates:

• Electrons are pushed onto the negative plate, which resists them because like charges repel.
• Electrons are also pulled away from the positive plate, which tries to pull them back.

This push and pull takes effort, and that effort becomes stored energy in the field between the plates.

🧠 Important Formulas:

Let’s say:

• The area of each plate is A
• The distance between plates is d
• The volume between the plates is A × d

Energy stored in the capacitor is:

 ½ × C × V²

So,
Energy Density (u) =

(½ × C × V²) ÷ (A × d)

This tells us how much energy is sitting inside that space between the plates.

Voltage Rating of a Capacitor

Every capacitor has a limit on how much voltage it can handle. This limit is called its voltage rating.

You can think of a capacitor like a balloon. Just as a balloon can hold only a certain amount of air before it bursts, a capacitor can hold only a certain amount of voltage before it gets damaged.

The voltage rating tells us the highest DC (direct current) voltage that can be safely given to the capacitor. If you give more voltage than the rating, the material inside the capacitor (called the dielectric) can break. When that happens, the capacitor may start to pass current like a wire, which is very dangerous and can permanently damage it.

That’s why it is very important to always check two things before using a capacitor:

1. Its capacitance – how much electric charge it can store.
2. Its voltage rating – the maximum voltage it can handle safely.

Using the right capacitor in the right way keeps your circuits safe and working properly.

Leakage Resistance of a Capacitor

A capacitor is like a tiny energy tank that stores electric charge. Inside it, there are two metal plates with a special material between them. This material is called the dielectric.

Now imagine if this material was perfect—like a wall so strong that nothing could pass through it. In that case, no current would flow through the material, even if you applied voltage. This would be called an ideal capacitor.

But in real life, nothing is truly perfect. The material in a real capacitor is a very good insulator, but not perfect. This means a tiny bit of current can still sneak through. This happens because the material has a very high resistance, but not infinite.

This resistance is called the leakage resistance.

It’s called “leakage” because just like water can leak from a bottle, a little bit of current can “leak” through the dielectric. The better the material, the higher the resistance, and the smaller the leak.

In a well-made capacitor, this leakage resistance is very, very high. That means almost no power is wasted, even when the capacitor is working with high voltage.

To understand it simply:

• If the resistance is low → more leakage → not a good capacitor.
• If the resistance is high → less leakage → better capacitor.

So, leakage resistance tells us how good the capacitor is at holding charge without letting current slip through where it shouldn’t.

Force Between Charged Plates

Imagine two flat metal plates placed facing each other.
They are very close to each other — just a few centimeters or maybe millimeters apart.
One plate has positive charge (+Q), and the other has negative charge (−Q).

Because opposite charges attract, there is a pulling force between these plates.
Let’s call this force F.

🧠 What Happens If We Move One Plate?

Now imagine you move one plate just a tiny bit farther away — we’ll call this small distance dx.

To do this, you need to apply some force, right?
So you’re doing work, and that work is:

Work = Force × Distance
→ Work done = F × dx

Now, here’s something very important:
Even though we moved the plate, the charges on both plates are still the same.
No charge came in or went out.

⚡ Where Does That Work Go?

That energy doesn’t disappear.
It gets stored inside the space between the plates, in the form of electrical energy.

This stored energy depends on something called capacitance (C), which is basically how well the plates can hold electric charge.

At first, the stored energy is:

Initial energy = (1/2) × Q² / C

When we move the plate a bit farther, the plates become less able to hold charge, so the capacitance decreases slightly.
Let’s call this small change dC.

Then the new capacitance becomes C − dC, and the stored energy becomes a little more, because the plates are holding the same charge but have less space to do it.

🔁 Connecting Work and Energy

Since energy can’t be created or destroyed,

Work done = Change in stored energy

When we calculate this change, we get:

Change in energy = (1/2) × Q² × dC / C²

So if we match this with the earlier formula for work (F × dx), we get:

F × dx = (1/2) × Q² × dC / C²

Which leads to:

Force, F = (1/2) × Q² × (dC/dx) / C²

🧪 Using Voltage Instead of Charge

We can also write this using voltage (V), because:

V = Q / C
So when we put that in, the formula becomes:

F = (1/2) × V² × (dC/dx)

📏 Capacitance Formula

Now, for two flat plates of area A, separated by distance x, and placed in air or a material, the capacitance is:

C = ε₀εᵣ × A / x

Where:

• ε₀ is a constant (called permittivity of free space)
• εᵣ is how well the material between the plates can hold electric field
• A is the area of the plates
• x is the gap between them

So when we find dC/dx, and put everything into the force formula, we get:

F = (1/2) × ε₀ × εᵣ × A × (V² / x²)
Or in air (where εᵣ = 1):
F = (1/2) × ε₀ × A × (V² / x²)

FAQ